Question

The length of a rectangular blackboard is 8 cm more than its breadth. If its length is increased by 7 cm and breadth is decreased by 4 cm, its area remains unchanged. Find the length and breadth of the rectangular blackboard.
A.28cm, 20cm
B.20cm, 24cm
C.24cm, 16cm
D.28cm, 16cm

Answer 1

Hint: The area of rectangle having length ‘x’ units and breadth ‘y’ units is ‘xy’ square units.
If length is increased by ‘m’ units and breadth is decreased by ‘n’ units and let’s say area is increased by ‘p’ units, then we can represent this as
$(x + m)(y - n) = xy + p$

Complete step-by-step answer:
Let length of rectangular blackboard be ‘x’ cm and breadth be ‘y’ cm

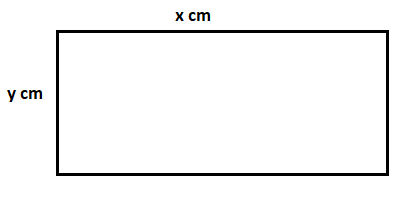
Now, first condition says that length of a rectangular blackboard is 8 cm more than its breadth which is written as : $x = y + 8$ --1
Second condition says that length is increased by 7 cm and breadth is decreased by 4 cm, its area remains unchanged which can be written as $(x + 7)(y - 4) = xy$
Put value of ‘x’ from equation 1; we get:
$\Rightarrow$ $(y + 8 + 7)(y - 4) = (y + 8)y$
$\Rightarrow$ $(y + 15)(y - 4) = (y + 8)y$
Now, multiply brackets, which will give us:
$\Rightarrow$ ${y^2} + 11y - 60 = {y^2} + 8y$
Cancelling ${x^2}$ on both sides, we get
$\Rightarrow$ $11y - 60 = 8y$
Which gives us value of $y = 20$
Put this value of ‘y’ in equation 1, we get;
$\Rightarrow$ $x = 20 + 8 = 28$
So, length of rectangular blackboard is 28 cm and breadth of rectangular blackboard is 20 cm
So, option (A) is correct.

Note: Every linear equation with two variables represents a line graphically such that each solution (x,y) of a linear equation $ax + by + c = 0$ corresponds to a point on the line representing the equation.