Question

The length of a rectangle is increased by 30% and the breadth is also increased by 30%. Then what is the effect on the area of the rectangle?
(A) Increases by 30%.
(A) Decreases by 30%.
(A) Decreases by 69%.
(D) Increases by 69%.

Answer 1

Hint: Let us assume the length of the rectangle as x and the breadth of the rectangle as y. Now, calculate the area of the rectangle using the formula, \[\text{Area=Length}\times \text{Breadth}\] . Now, we have a new rectangle in which the length of the rectangle is increased by 30% and the breadth is also increased by 30%. The new length of the rectangle is (x + 30% of x). The new breadth of the rectangle is (y + 30% of y). Now, get the area of the new rectangle using the formula, \[\text{Area=Length}\times \text{Breadth}\] . Then, subtract it from the area of the original rectangle. Solve it further and calculate the percentage.

Complete step-by-step answer:
According to the question, it is given that there is a rectangle and the length of the rectangle is increased by 30% and the breadth is also increased by 30%. We have to find the effect of this change on the area of the rectangle.

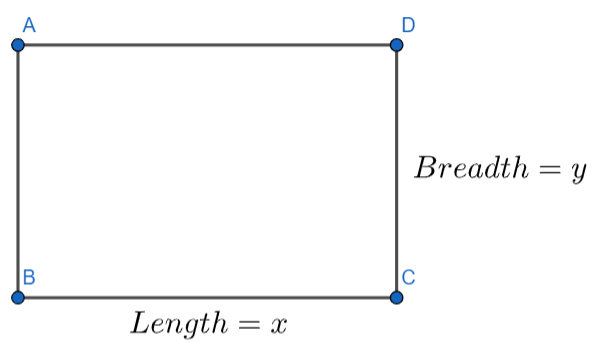
Let us assume the length of the rectangle be x and the breadth of the rectangle be y.
The length of the rectangle = x ………………..(1)
The breadth of the rectangle = y ………………….(2)
We know the formula of the area of a rectangle, \[\text{Area=Length}\times \text{Breadth}\] …………………(3)
Putting the value of the length and breadth of the rectangle from equation (1) and equation (2) in equation (3), we get
 \[\begin{align}
  & \text{Area=Length}\times \text{Breadth} \\
 & \text{Area=}x\times y \\
\end{align}\]
\[\text{Area}=xy\] …………………(4)
Now, the length of the rectangle is increased by 30% and the breadth is also increased by 30%.

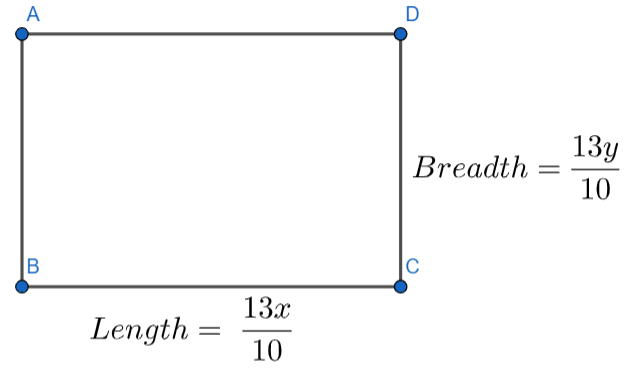
The new length of the rectangle = x + 30% of x = \[x+\dfrac{30}{100}x=\dfrac{100x+30x}{100}=\dfrac{130}{100}x=\dfrac{13x}{10}\] …………………….(5)
The new breadth of the rectangle = y + 30% of y = \[y+\dfrac{30}{100}y=\dfrac{100y+30y}{100}=\dfrac{130}{100}y=\dfrac{13y}{10}\] …………………….(6)
Putting the value of the length and breadth of the rectangle from equation (5) and equation (6) in equation (3), we get
 \[\begin{align}
  & \text{Area=Length}\times \text{Breadth} \\
 & \text{Area=}\dfrac{13x}{10}\times \dfrac{13y}{10} \\
\end{align}\]
\[\text{Area}=\dfrac{169xy}{100}\]
So, the area of the new rectangle is \[\dfrac{169xy}{100}\] ………………(7)
From equation (4) and (7), we have the area of the rectangle and the area of the new rectangle respectively.
The Increment in Area of the rectangle = Area of new rectangle – Area of the rectangle
\[\begin{align}
  & =\dfrac{169xy}{100}-xy \\
 & =\dfrac{169xy-100xy}{100} \\
 & =\dfrac{69xy}{100} \\
\end{align}\]
The Increment in Area of the rectangle is \[\dfrac{69xy}{100}\] .
Therefore, the percentage of increment in area of the rectangle = \[\dfrac{\dfrac{69xy}{100}}{xy}\times 100=\dfrac{69xy}{100\times xy}\times 100=69\] .
Hence, the correct option is (D).

Note: In this question, while calculating the percentage one might divide \[\dfrac{69xy}{100}\] by \[\dfrac{169xy}{100}\] and then multiply it by 100. This is wrong. We cannot divide by \[\dfrac{169xy}{100}\] because we have to find the percentage of change of area with respect to the area of the original rectangle. So, we have to divide \[\dfrac{69xy}{100}\] by \[xy\] and then it by 100.