Question

The length of a rectangle exceeds its breadth by 5 cm. Two vertices of a triangle coincide with that of the rectangle and the third vertex lies on the opposite side of the rectangle. The area of the remaining part is
a. Half of that of the rectangle
b. One-third that of that the rectangle
c. One-fourth that of that the rectangle
d. None of these

Answer 1

Hint: According to the given question, firstly assume the length of the rectangle to be x cm and as it is given breath exceed by 5 cm so breadth = \[x + 5\] .Then calculate the area of triangle \[ = \dfrac{1}{2} \times b \times h\] as well as area of rectangle .After that find out the area of remaining part is equal to area of rectangle \[ - \] area of triangle which is required answer.

Complete step-by-step solution:
As, it is given that the length of the rectangle exceeds its breadth by 5 cm.

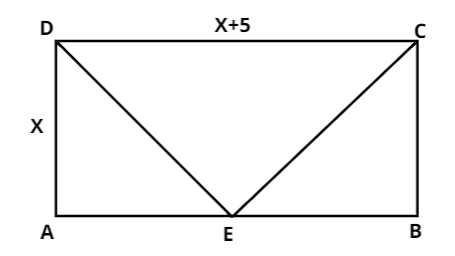
Let, the length of the rectangle be x.
According to condition, length exceeds breadth by 5 cm.
Therefore, length = x and breadth = \[x + 5\]
Now,
Area of triangle (D E C) is
\[a = \dfrac{1}{2} \times x \times (x + 5)\]
\[ = \,\dfrac{{x(x + 5)}}{2}\]
Now,
Area of the rectangle (A B C D) is \[x(x + 5)\] , where x is the length and (x + 5) is the breadth.
Then,
Subtracting the area of the triangle from the area of the rectangle we will get the area of the remaining part.
Therefore, Area of rectangle A B C D= \[x(x + 5)\]
Area of triangle D E C = \[\dfrac{1}{2} \times x \times (x + 5)\]
Therefore, Area of remaining part = Area of rectangle – Area of triangle
\[x(x + 5)\, - \,\dfrac{1}{2} \times x \times (x + 5)\]
\[ = \,\dfrac{1}{2}[x(x + 5)]\]
Therefore, the answer is half of that of the rectangle.

Thus, option (a) is correct.

Note: These types of questions can come in the form of a square inside a triangle , circle inside a square and also in the form of a shaded portion. You just need to remember that the shapes you are given with just calculate their areas by using the specified formulas. Hence by observing the figure calculate the remaining portion or shaded portion which have been asked in the question.