Question

The length of a 10cm high cuboid exceeds its breadth by 4cm. If the volume of the cuboid is \[2210c{m^3}\]. Find its lateral surface area.

Answer 1

Hint: At first we will assume the breadth of the cuboid to be x, then we’ll get the length of the cuboid in terms of breadth. Then we’ll substitute all these measurements in the formula of the volume of a cuboid from where we’ll get the actual measurements of length and breadth.
Now we can easily find the lateral surface area of the cuboid using its formula, to get the required answer.

Complete step by step solution:
Given data: The height of the cuboid $ = 10cm$
The volume of the cuboid \[ = 2210c{m^3}\] .
Length of the cuboid exceeds its breadth by 4cm

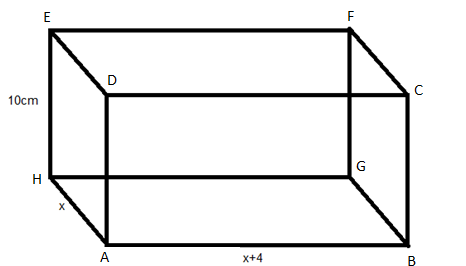
Let the breadth of the cuboid be x cm
Therefore according to the given data, the length of the cuboid will be $\left( {x + 4} \right)cm$
We know that the volume of the cuboid \[ = length \times breadth \times height\]
Substituting the value of volume and length, breadth, and height
 \[ \Rightarrow 2210 = \left( {x + 4} \right)x \times 10\]
Dividing both sides by 10, we get,
 \[ \Rightarrow 221 = \left( {x + 4} \right)x\]
On factoring 221, we get,
 \[ \Rightarrow 17 \times 13 = \left( {x + 4} \right)x\]
On comparing the left-hand side and right-hand side, we can say that \[x = 13\]
Therefore breadth of the cuboid \[ = 13cm\]
And the length of the cuboid \[ = 17cm\]
Now using the formula for the lateral surface area of the cuboid i.e. $2height(length + breadth)$
The lateral surface area of the given cuboid $ = 2 \times 10(13 + 17)$
 $ = 20(30)$
On simplifying, we get,
 $ = 600c{m^2}$
Therefore the required lateral surface area of the cuboid is $600c{m^2}$.

Note: Most of the students think 10cm as the length of the cuboid which is not the correct but it is the height of the cuboid, we should understand the question properly before solving it as if we take the measurements incorrect the required aspect i.e. lateral surface area will be incorrect too.