Question

The length, breadth and height of a room are 850 cm, 625 cm and 475 cm. Find the length of the longest rod that can measure the dimensions of the room exactly.

Answer 1

Hint: For solving this problem we should know that to find the length of rod that can measure the dimensions of the room exactly then, the length of that rod will be the common factor of length, breadth and the height of the room. And for the longest length of such rod then, the length will be the HCF (highest common factor) of the dimensions of the room.

Complete step-by-step answer:

Given:
A room of length 850 cm, breadth 625 cm and height of 475 cm as shown in the figure below:

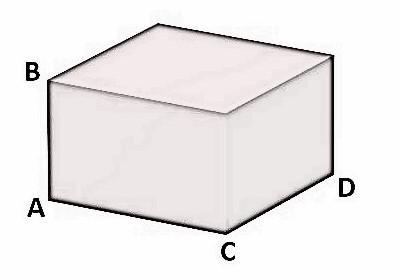
In the above figure,
Length of the room is AC = 850 cm.
Breadth of the room is CD = 625 cm.
Height of the room is AB = 475 cm.

Now, we have to find the length of the longest rod which will measure the dimensions of the room exactly then, the length of such rod will be the HCF of length, breadth and height of the room. So, we have to find the HCF of 850, 625 and 475. First, we will find the factors of 850, 625 and 475 then we can find their HCF.

Factors of 850.
We can write, $850=1\times 2\times 5\times 5\times 17$ .
Then, factors of 850 are 1, 2, 5, 17, 10, 25, 34, 50, 85, 170, 425, 850.

Factors of 625:
We can write, $625=1\times 5\times 5\times 5\times 5$ .
Then, factors of 625 are 1, 5, 25, 125, 625.

Factors of 475:
We can write, $475=1\times 5\times 5\times 19$ .
Then, factors of 475 are 1, 5, 19, 25, 95, 475.

Now, from the factors of 850, 625 and 475 we can find that their HCF will be 25. Then, the length of the longest rod which will measure the dimensions of the room exactly will be 25 cm.

Thus, the length of the rod will be 25 cm.

Note: The question is very easy to solve but one should be able to crack the point that HCF of the length, breadth and height will be the length of the longest rod which will measure the dimensions exactly. Then, only find the HCF without any calculation mistakes.