Question

The length, breadth and height of a godown are 15 m, 12 m and 9 m respectively. Cubic blocks of side 3 m are placed in the godown. Find how many blocks can be placed in the godown.

Answer 1

Hint: The length, breadth and height of a godown are given. Therefore find its volume. Now cubic blocks of side 3 m are placed in the godown. Find the volume of each cubic block. Now, suppose the godown can be filled up with n such cubic blocks.
Therefore, the total volume of n cubic blocks will be equal to the capacity of the godown

Complete step-by-step answer:
We know that when the dimensions are mentioned, the volume of a cuboid and that of a cube are given as follows,

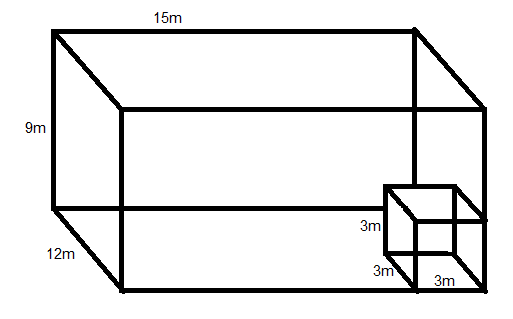
Given that, the length, breadth and height of a godown are 15 m, 12 m and 9 m respectively.
Therefore, the capacity (volume) of the godown is,
$ = 15 \times 12 \times 9\,\,{{\text{m}}^{\text{3}}}$
On multiplication we get,
$ = 1620\,\,{{\text{m}}^{\text{3}}}$
Now, cubic blocks of side 3 m are placed in the godown.
Therefore, volume of each cubic block is
$ = {\left( 3 \right)^3}\,\,{{\text{m}}^{\text{3}}}$
On cubing we get,
$ = 27\,\,{{\text{m}}^{\text{3}}}$
In other words, each cubic block takes up a space of $27\,{{\text{m}}^{\text{3}}}$
Suppose, the godown can be filled up with n cubic blocks.
Therefore, the total volume of n cubic blocks will be equal to the capacity of the godown.
$ \Rightarrow n \times 27 = 1620$
On dividing the equation by 27, we get
$ \Rightarrow n = \dfrac{{1620}}{{27}}$
On simplification we get,
$ \Rightarrow n = 60$
Hence, 60 blocks can be placed in the godown.
Note: We must make sure that the dimensions of the cuboid are the multiples of the length of the side of the cube. If it is not, then we cannot place the cube completely. We need to either cut the cube or leave the remaining space.
Alternate solution to this problem is given by,
We have the length of the go down as 15m and the cube has a length of 3m.
So, the number of cubes that can be placed lengthwise is given by, $\dfrac{{15}}{3} = 5$
We have the width of the go down as 12m and the cube has a length of 3m.
So, the number of cubes that can be placed width wise is given by, $\dfrac{{12}}{3} = 4$
We have the height of the go down as 9m and the cube has a length of 3m.
So, the number of cubes that can be placed height wise is given by, $\dfrac{9}{3} = 3$
So, the total number of cubes that can be placed inside the go down is given by taking their product,
 $ \Rightarrow n = 5 \times 4 \times 3$
On simplification we get,
 $ \Rightarrow n = 60$
Hence, 60 blocks can be placed in the go down.