Question

The length and breadth of a rectangular park are in the ratio 8:5. A path 1.5 m wide running all around the outside of the park has an area of 594 ${{m}^{2}}$ . Find the dimensions of the park.

Answer 1

Hint: From given problem, we get the ratio of length and breadth of a rectangular path is 8:5, from this indication, we will get clear message to find two values like length and breadth that we can take one constant variable x in given proportion, i.e 8x and 5x. Then, we can calculate the area of the park in terms of x. Next, we calculate the area of the park along the path. Here, the area of the path is given in question. So, area of park = area of park along with path – area of path. By comparing these equations, we will get the value of x. Now, we will get values of dimensions of the park in terms of length and breadth.

Complete step by step answer:
Since we have been given the ratio of park length and breadth as 8:5, we can write that
Let the length of the park, rectangle ABCD be 8x m
Let the breadth of the park, rectangle ABCD be 5x m
By using the length and breadth of park rectangle, we will get area
Area = length $\times $ breadth
Therefore, we get the area of rectangle ABCD
\[\begin{align}
  & =(8x\times 5x)m \\
 & =40{{x}^{2}}{{m}^{2}} \\
\end{align}\]
Let us consider that a path PQRS, 1.5 m wide runs all around the outside of the park as given in the question,

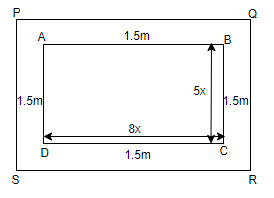
Now, we can first find the length and breadth of rectangle PQRS.
Therefore, we get the length of the park including path PQRS as
\[\begin{align}
  & =8x+2\left( \text{width of path} \right) \\
 & =8x+2(1.5) \\
 & =\left( 8x+3 \right)m \\
\end{align}\]
Similarly we can find out breadth of the park including path PQRS as
\[\begin{align}
  & =5x+2\left( \text{width of path} \right) \\
 & =5x+2(1.5) \\
 & =\left( 5x+3 \right)m \\
\end{align}\]
Now, we can find the area of the park including path PQRS by multiplying the length and breadth as
\[\begin{align}
  & =(8x+3)(5x+3) \\
 & =(40{{x}^{2}}+39x+9){{m}^{2}} \\
\end{align}\]
This area is the area of the park along the path.
We have been given that the area of the path running outside the park is 594 ${{m}^{2}}$ . So, we can form the equation as below,
Area of park along with path, i.e. PQRS - Area of park, i.e. ABCD = 594 ${{m}^{2}}$
Substituting above obtained results, we have
\[\begin{align}
  & \Rightarrow 40{{x}^{2}}+39x+9-40{{x}^{2}}=594 \\
 & \Rightarrow 39x=594-9 \\
 & \Rightarrow 39x=585 \\
 & \Rightarrow x=\dfrac{585}{39} \\
 & \Rightarrow x=15 \\
\end{align}\]
Since we know that the length of the park = 8x, we can substitute values of x as
\[\begin{align}
  & =8\times 15 \\
 & =120m \\
\end{align}\]
Similarly, we can find breadth of the park = 5x as
\[\begin{align}
  & =5\times 15 \\
 & =75m \\
\end{align}\]

Therefore, we have got the length of the park as 120m and the breadth of the park as 75m.

Note: Drawing a figure for better understanding plays an important role in these types of problems. Students usually get confused between rectangle ABCD and PQRS. Here, we have been given the area of path as 594 ${{m}^{2}}$ , so it is the difference between area of PQRS and area of ABCD. This must be taken care of. If students don’t understand this, they may form an equation as : Area of park along with path PQRS = 594 ${{m}^{2}}$ and then solve for x from this.