Question

The length and breadth of a rectangular hall are $0.4m$ and $30cm$ respectively. The distance between two opposite corners of the hall is______.
A. $34.16m$
B. $50m$
C. $34.16cm$
D. $50cm$

Answer 1

Hint: Here we are given the length and breadth of a rectangle and we are asked to find the distance between two opposite corners of a rectangle. The distance between two opposite corners of the rectangle is nothing but the distance of the diagonal. That is we need to calculate the distance of the diagonal.

Formula used:
The formula to calculate the distance of the diagonal of a rectangle is as follows.
The distance of the diagonal of a rectangle is $ = \sqrt {lengt{h^2} + breadt{h^2}} $

Complete step by step solution:
Let $l$ be the length of a rectangular hall and $b$ be the breadth of a rectangle.
It is given that the length of a rectangle is $l = 0.4m$ and the breadth of the rectangle $b = 30cm$.
Before getting into the solution, we need to convert the given values of length and breadth into the same units.
We shall convert the length of a rectangle into centimeters.
That is, $l = 0.4m$
$l = 0.4 \times 100cm$
$ \Rightarrow l = 40cm$
Therefore the length of a rectangle is $l = 40cm$
Here we are asked to calculate the distance between two opposite corners of the hall.

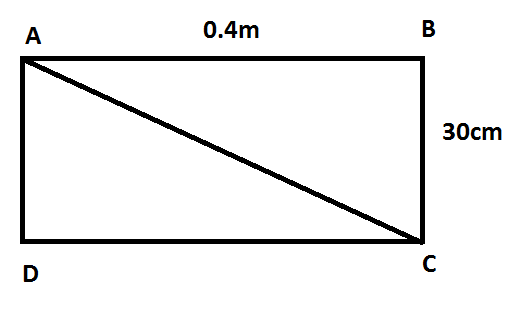
If ABCD is a rectangle, then we need to find the distance between two opposite corners of the rectangle. That means we have to find the distance of the diagonal AC.
We need to apply the given values of length and breadth in the formula (The distance of the diagonal of a rectangle $ = \sqrt {lengt{h^2} + breadt{h^2}} $
The distance between the two opposite corners of the hall is $ = \sqrt {lengt{h^2} + breadt{h^2}} $
 $ \Rightarrow \sqrt {{{40}^2} + {{30}^2}} $
On simplification,
$ \Rightarrow \sqrt {1600 + 900} $
$ \Rightarrow \sqrt {2500} $
On solving the square root,
$ \Rightarrow \sqrt {50 \times 50} = 50$
Therefore the distance between two opposite corners of a hall is $50cm$. Hence, option (D) is correct.

Note:
Before getting into the solution, we have to check whether the given values are in the same units or not. If not, our first step is to convert them. Since the given values of length and breadth of a rectangle do not contain the same units, we convert them into centimeters.