Question

The length and breadth of a rectangular field is \[110m\] and \[30m\] respectively. Calculate the length of the longest rod which can measure the length and breadth of the field exactly.

Answer 1

Hint: In this question, we have to find out the length of the longest rod which can measure the given length and breadth of the rectangle.
We need to first factorize the length and breadth of the rectangle then find out the H.C.F of the two of them because H.C.F. is the greatest number which divides each of the two numbers, thus this is the required result.

Complete step-by-step answer:
It is given that the length and breadth of a rectangular field is \[110m\] and \[30m\] respectively.
We need to find out the length of the longest rod which can measure the length and breadth of the field exactly.
Now, we need to first factorize the length and breadth.
Factoring we get,
The length is \[110m\] and \[110 = 2 \times 5 \times 11\].
The breadth is \[30m\] and \[30 = 2 \times 3 \times 5\].
To find the length of the longest rod which can measure the length and breadth of the field exactly we need to find the H.C.F of the length and breadth of the rectangle because H.C.F. is the greatest number which divides each of the two numbers.
Thus the H.C.F. of \[110\] and \[30\] is \[2 \times 5 = 10\] because these are the only common terms between two of them.

Hence, the length of the longest rod which can measure the length and breadth of the field exactly is \[10m\].

Note: Highest common factor or H.C.F.:
In mathematics, the Highest common factor or, greatest common divisor of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers.
We can factorize the length and breadth in Tree method,
That is,

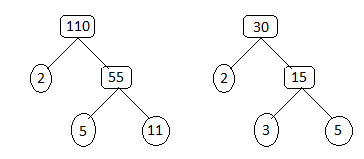
Factoring we get,
The length is \[110m\] and \[110 = 2 \times 5 \times 11\].
The breadth is \[30m\] and \[30 = 2 \times 3 \times 5\].
Thus the H.C.F. of \[110\] and \[30\] is \[2 \times 5 = 10\] because these are the only common terms between two of them.
Hence, the length of the longest rod which can measure the length and breadth of the field exactly is \[10m\].