Question

The length and breadth of a rectangular field are $120{\text{ }}m$ and $80{\text{ }}m$ respectively. Inside the field, a park of $12{\text{ }}m$ width is made around the field. The area of the park is?
A) $3224{\text{ }}{m^2}$
B) $7344{\text{ }}{m^2}$
C) $2256{\text{ }}{m^2}$
D) $4224{\text{ }}{m^2}$

Answer 1

Hint: First we will calculate the area of the rectangular field using the original dimensions. After that, we will calculate the effective area of the field apart from the park. Then, we will be in a position to the area of the park.

Complete step-by-step answer:
Below is the schematic diagram of the field and park:

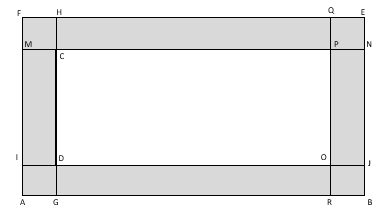
Rectangular Field (Park – Shaded Region)
Complete step-by-step solution:
In the figure, we can see the original boundary of the field, $ABEF$ . Also, we can see the new smaller boundary, $DOPC$, after the park (shaded region) is excluded.
Let us write down dimensions of line segments in the figure below:
$AB\,\, = \,\,EF\,\, = \,\,120m$ (original length)
$AF\,\, = \,\,BE\,\, = \,\,80m$ (original breadth)
$DG = PN = QP = MC = DI = AI = EN = HC = MF = 12m$ (width of the park)
Dimensions of the new field:
$DO = PC = AB - 2 \times DI = 120 - 2 \times 12 = 120 - 24 = 96m$
$OP = CD = AF - 2 \times AI = 80 - 2 \times 12 = 80 - 24 = 56m$
Calculation of Areas:
$Area{\text{ }}of{\text{ }}the{\text{ }}original{\text{ }}field{\text{ }}\left( {before{\text{ }}park} \right)\;\; = \,\,AB\,\, \times \,\,AF\,\, = \,\,120 \times 80\,\, = \,\,9600\,{\text{ }}{m^2}$
$Area{\text{ }}of{\text{ }}the{\text{ }}new{\text{ }}field{\text{ }}\left( {after{\text{ }}park} \right)\;\;\;\;\;\;\;\;\;\;\;\; = \,\,\,DO\,\, \times \,\,OP\,\, = \,\,96\,\, \times \,\,56\,\, = \,\,5376\,{\text{ }}{m^2}$
\[\therefore \,\;Area{\text{ }}of{\text{ }}the{\text{ }}park{\text{ }} = {\text{ }}Area{\text{ }}of{\text{ }}the{\text{ }}original{\text{ }}field{\text{ }} - {\text{ }}Area{\text{ }}of{\text{ }}the{\text{ }}new{\text{ }}field\]
\[ \Rightarrow \,\;Area{\text{ }}of{\text{ }}the{\text{ }}park{\text{ }} = {\text{ }}\left( {{\text{9600}}\, - 5376} \right)\,{\text{ }}{{\text{m}}^2}\]
\[ \Rightarrow \,\;Area{\text{ }}of{\text{ }}the{\text{ }}park{\text{ }} = {\text{ 4224 }}{{\text{m}}^2}\]

Therefore, option (D) is correct.

Note: This problem could have been directly solved using a different method if this question would have been asked in a competitive exam.
If we closely observe the figure, we can see 4 squares of side length as 12m at the corners.
Also, we see two parallel rectangles DORG and HQPC with length and breadth respectively as 96 m and 12 m. Additionally, we see two parallel rectangles MCDI and PNJO with length and breadth respectively as 56 m and 12 m.
\[\therefore \,\;Area{\text{ }}of{\text{ }}the{\text{ }}park{\text{ }} = {\text{ 2}} \times {\text{(96}} \times {\text{12) + 2}} \times {\text{(56}} \times {\text{12)}} + 4 \times 12 \times 12\]
\[ \Rightarrow \,\;Area{\text{ }}of{\text{ }}the{\text{ }}park{\text{ }} = {\text{ 4224 }}{{\text{m}}^2}\]