Question

The least number to be subtracted from $16800$ to make it a perfect square, is
A) $249$
B) $159$
C) $169$
D) $219$

Answer 1

Hint:
We will use a division method to find the square root. Make a pair of two digits from the right to left of $16800$. Check that the quotient should be less than the remainder for perfect square. Subtract the obtained remainder from the given number to make it a perfect square.

Complete step by step solution:
We know that to find the least number that needs to be subtracted from the given number to make it perfect square, use the long division method.

To find the square root of the given number by using a long division method, we need to make a pair of two digits from right to left as $\overline 1 \;\overline {68} \;\overline {00} $.

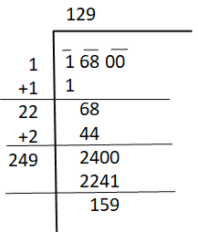
We get that the remainder is $159$ and the quotient is $129$.
The square of obtained quotient is:
${\left( {129} \right)^2} = 16641$
From the above result we can say that the square of $129$ is a number less that is $159$ less than the given number $16800$.
We will subtract $159$ from $16800$ to get a perfect square number.
The least number that should be subtracted from $16800$ to make it a perfect square is $159$.

Therefore, the option (B) is correct.

Note:
We can use an alternative method to use the number that should be subtracted from the given number to make it perfect square. We need to find a number whose square is greater than 16800 and a number whose square is less than 16800. Now, subtract the square numbers, the resulting number is the required result.
Make sure that the remainder should be subtracted from the given number. Do not add the remainder otherwise this may lead to incorrect answers.