Question

The lateral surface area of a hollow cylinder is \[5632c{m^2}\] . It is cut along its height and a rectangular sheet of width 44cm is formed. Find the perimeter of the rectangular sheet?
A.344cm
B.388cm
C.320cm
D.300cm

Answer 1

Hint: The lateral surface area of cylinder is $2\pi rh$ where ‘r’ is radius of cylinder and ‘h’ is height of cylinder. When a cylinder is cut along its height then it will make a rectangular sheet having breadth is equal to height of cylinder and length is equal to perimeter of top of cylinder.

Complete step-by-step answer:

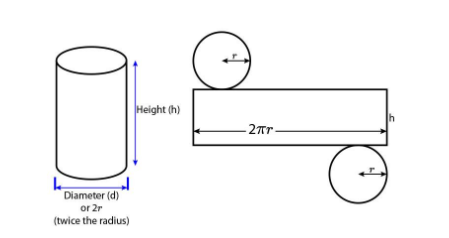
We have a cylinder with radius ‘r cm’ and height ‘h cm’.
It is given that lateral surface area of cylinder is \[5632c{m^2}\]
So; $2\pi rh = 5632$
On putting values, we get: $2 \times \dfrac{{22}}{7} \times r \times h = 5632$
On solving, we get: $rh = \dfrac{{5632 \times 7}}{{2 \times 22}}$
It gives us $rh = 896$ ---(1)
Now, it cut along its axis and rectangular sheet is formed as in figure:
So, width of sheet (x) = Perimeter of top of cylinder = $2\pi r$
 Length of sheet = 44cm = height of cylinder(h)
So, $(2\pi r)h = 5632$
Put $2\pi r = x$ and $h = 44$
We get a value of $x = 128$ which is the width of a rectangular sheet.
So, Perimeter of Sheet is $2(x + h) = 2(128 + 44) = 2(172) = 344$ cm
So, Perimeter is 344 cm

Note: The difference is lateral or curved surface area of cylinder and total surface area of cylinder is that in curved surface area, area of top and bottom surfaces are not included but in total surface area, they are included.