Question

The internal dimensions of a box are 1.2 m, 80 cm, and 50 cm. How many cubes each of edge 7 cm can be packed in the box with faces parallel to the sides of the box. Also, find the space left empty in the box.
(a) $1229;31,283\text{ c}{{\text{m}}^{3}}$
(b) $1309;31,013\text{ c}{{\text{m}}^{3}}$
(c) $1169;31,163\text{ c}{{\text{m}}^{3}}$
(d) none of the above

Answer 1

Hint: For solving this question first we will draw the figure of the box and after that, we will consider one rectangular base and try to figure out that how many cubes of 7 cm can be placed in one layer and after that we will find how many such layers can be placed. Then, we will answer this question easily.

Complete step-by-step solution -
Given:
It is given that there is a box having internal dimensions 1.2 m, 80 cm, and 50 cm and we have to find the number of cubes of edge 7 cm can be packed in the box with faces parallel to the sides of the box and how much space is left in the box.
Now, to visualize the box with dimensions 1.2 m or 120 cm, 80 cm, and 50 cm look at the figure given below:

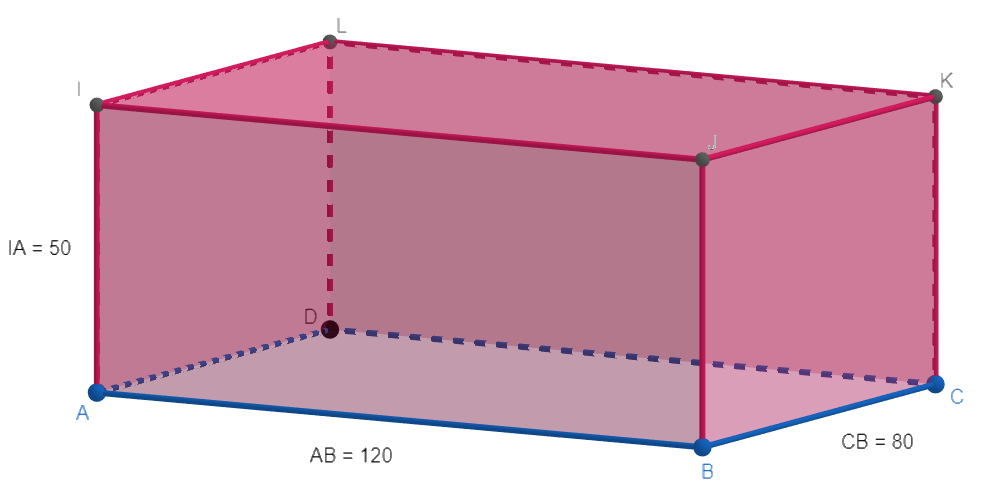
Now, here take the base rectangle of side 120 cm and 80 cm and try to place cubes of 7 cm on it one by one and let’s see in one layer we can place how many such cubes.
Now, when we place cubes of 7 cm along the side of 80 cm then will at max place 11 cubes as 11 cubes will occupy $11\times 7=77$ cm of 80 cm and after that when we place cubes along the side of 120 cm then we will at max place 17 cubes as 17 cubes will occupy $17\times 7=119$ cm of 120 cm. For more clarity look at the figure given below:

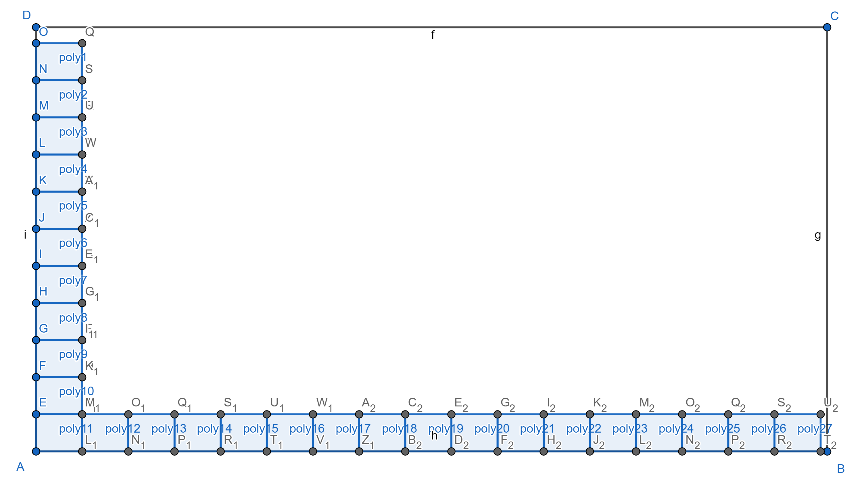
Now, from the above figure, we conclude that on the base rectangle of side 120 cm and 80 cm we can at max place $11\times 17=187$ cubes in one layer. And as the cube edge is of 7 cm and one layer will occupy 7 cm of 50 cm height, so we can place at max 7 such layers as 7 layers will occupy $7\times 7=49$ cm of the 50 cm height.
Now, we conclude that we can place at max $11\times 17\times 7=1309$ cubes of edge 7 cm in the box having internal dimensions 1.2 m, 80 cm, and 50 cm.
Now, the volume of the box $=\left( \text{length} \right)\times \left( \text{breadth} \right)\times \left( \text{height} \right)=120\times 80\times 50=480000\text{ c}{{\text{m}}^{3}}$ .
And volume of 1309 cubes of edge 7 cm $=1309\times {{\left( \text{edge length} \right)}^{3}}=448987\text{ c}{{\text{m}}^{3}}$ .
Now, we can see that the space left in the room will be the difference of the above two volumes. Then,
Space left in the room $=480,000-448,987=31,013\text{ c}{{\text{m}}^{3}}$ .
Now, we conclude that we can place at max 1309 cubes of 7 cm edge length and there will be $31,013\text{ c}{{\text{m}}^{3}}$ space left in the room.
Hence, (b) is the correct option.

Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer. After that, we should draw figures and diagrams for better understanding and solve with our intelligence to get the correct answer. Moreover, don’t directly divide the volume of the box with the volume of the cube to get the number of cubes directly. It would be a wrong approach and we will get the wrong answer.