Question

The interior dimensions of a rectangular fish tank are 4ft long, 3ft wide and 2ft high. The water level in the tank is 1ft high. All of the water in this tank is poured into an empty second tank. If the interior dimensions of the second tank are 3ft long, 2ft wide and 4ft high, what is the height of the water in the second tank?
A. 0.5ft
B. 1ft
C. 1.5ft
D. 2ft

Answer 1

Hint: Volume of a rectangular fish tank is \[l\times b\times h\] where \[l\] is the length, \[b\] is the width and \[h\] is the height of the tank. Water volume of the first tank and the water volume of the second tank will be the same as all of the water in the first tank is poured into an empty second tank. We have to use this formula to calculate the volume of water in the first fish tank and then further evaluate it accordingly.

Complete step-by-step answer:
Initially in the question the dimensions of a rectangular fish tank are given.
In the first fish tank the length of the tank is 4ft
The Width of the tank is 3ft and height is 2ft.
But the water level in the tank is 1ft high.

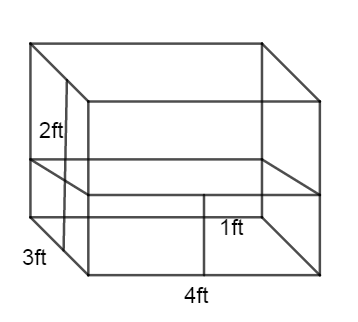
The volume of water is \[v=l\times b\times h\text{ f}{{\text{t}}^{3}}\] where \[l\] is the length, \[b\] is the width and \[h\] is the height of the tank.

According to the formulae the initial volume of the water in the fish tank is
\[\begin{align}
  & v=4\times 3\times 1\text{ f}{{\text{t}}^{3}} \\
 & \Rightarrow v=12\text{ f}{{\text{t}}^{3}} \\
\end{align}\]

The volume of water that is poured into the second fish tank is \[12\text{ f}{{\text{t}}^{3}}\].
Length, width and height of the second water tank is 3ft, 2ft and 4ft respectively.
Let us assume that the height of the water in the second tank is \[x\] ft.

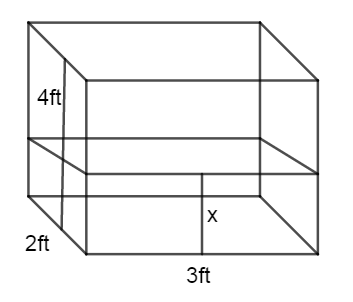
As water from the first tank is poured into the second tank, the volume of water will be the same.
By that we can create an equation,
\[\begin{align}
  & l\times b\times h=v \\
 & \Rightarrow 3\times 2\times x=12 \\
 & \Rightarrow 6x=12 \\
 & \Rightarrow x=\dfrac{12}{6} \\
 & \Rightarrow x=2 \\
\end{align}\]
The height of the water in the second tank is 2ft. (Option D).

Note: Students may get confused and calculate the total volume of the fish tank as length, width and height is provided in the question but we don’t need to do it. Water height is all that matters. So we have to work on the only water volume present in the fish tank. Students often forget to draw a diagram of a fish tank, sometimes diagrams help students to understand how to proceed further.