Question

The image of an object, formed by a plano-convex lens at a distance of 8 m behind the lens, is real and is one-third the size of the object. The wavelength of light inside the lens is \[\dfrac{2}{3}\] times the wavelength in free space. The radius of curved surface of the lens is:
A. 1 m
B. 2 m
C. 3 m
D. 6 m

Answer 1

Hint: In this question we are asked to calculate the radius of curved surface of lens. We know that this can be calculated using the formula of focal length for a plano-convex lens. It gives the relation between focal length, the index of refraction and radius of curved surface. Therefore, we will be calculating the index of refraction, as it is unknown to us.
Formula Used:
\[\dfrac{1}{f}=\dfrac{\left( \mu -1 \right)}{R}\]
\[\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}\]
\[\mu =\dfrac{{{\lambda }_{a}}}{{{\lambda }_{m}}}\]

Complete answer:
From the lens formula
       

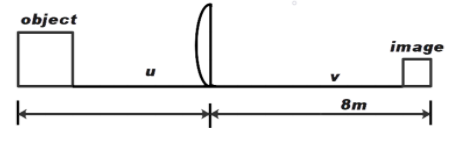
We know,
\[\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}\] …………… (1)
We also know that, focal length for plano-convex lens is also given by,
\[\dfrac{1}{f}=\dfrac{\left( \mu -1 \right)}{R}\] …………. (2)
Therefore, from (1) and (2)
We get,
\[\dfrac{\left( \mu -1 \right)}{R}=\dfrac{1}{v}-\dfrac{1}{u}\] ……………… (3)
Now, we know that refractive index I given by,
\[\mu =\dfrac{{{\lambda }_{a}}}{{{\lambda }_{m}}}\] ……………… (4)
Now, it is given that the wavelength in a lens is \[\dfrac{2}{3}\] times the wavelength in air. Therefore,
\[{{\lambda }_{m}}=\dfrac{2}{3}{{\lambda }_{a}}\]
After substituting the above value in equation (4)
We get,
\[\mu =\dfrac{3}{2}=1.5\] …………… (5)
Now, it is given that the size of image is \[\dfrac{1}{3}\] the size of object
Therefore, we can write
\[I=\dfrac{1}{3}O\]
Now from magnification formula we know,
\[M=\dfrac{I}{O}=-\dfrac{v}{u}\]
After substituting values
We get,
\[\dfrac{\dfrac{1}{3}O}{O}=-\dfrac{v}{u}\]
Therefore,
\[v=-\dfrac{1}{3}u\]
It is also given that the image is formed at a distance of 8 m i.e. \[v=8\]
Therefore,
\[u=-24\] …………….. (6)
After substituting the values of (5) and (6) in equation (3)
We get,
\[\dfrac{\left( 1.5-1 \right)}{R}=\dfrac{1}{8}-\dfrac{1}{(-24)}\]
On solving,
We get,
\[R=3\]

Therefore, the correct answer is option C.

Note:
A plano-convex lens is an optical device that has one curved surface and one plane surface. These lenses are used to focus the infinitely parallel rays of light at a point. The plano-side of the lens acts as a focus or point source. The real images are formed by converging the parallel rays. On the other hand, virtual images occur where the rays only appear to diverge. Real images can be projected on a screen unlike virtual images.