Question

The hypotenuse of a right-angled triangle is 25 cm. The other two sides are such that one is 5 cm longer than the other. Their lengths (in cm) are:
1) 10, 15
2) 20, 25
3) 15, 20
4) 25, 30

Answer 1

Hint: First, we will find the length of other sides. Then use the Pythagorean theorem on the sides of triangle and the property \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\] to simplify the equation. Then we will factor the equation to find the value of \[x\].

Complete step-by-step answer:

It is given that the hypotenuse is 25 cm.

Let the other two sides are \[x\] and \[x + 5\] respectively.

First, we will draw the triangle where the hypotenuse is 25 cm, the height is \[x\] cm and the base is \[x + 5\] cm.

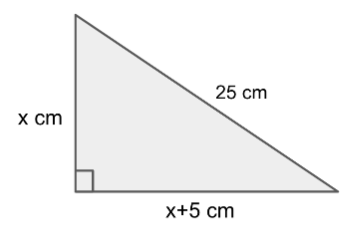
We know that the Pythagorean theorem \[{h^2} = {a^2} + {b^2}\], where \[h\] is the hypotenuse, \[a\] is the height and \[b\] is the base of the triangle.

Using the Pythagorean theorem on the given sides of the right-angled triangle, we get

\[{x^2} + {\left( {x + 5} \right)^2} = {25^2}\]

Using the property \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\] in the above equation, we get

\[
   \Rightarrow {x^2} + {x^2} + 10x + 25 = 625 \\
   \Rightarrow 2{x^2} + 10x + 25 = 625 \\
   \Rightarrow 2{x^2} + 10x - 600 = 0 \\
\]

We will now factor the above equation,

\[
   \Rightarrow 2{x^2} + 40x - 30x - 600 = 0 \\
   \Rightarrow 2x\left( {x + 20} \right) - 30\left( {x + 20} \right) = 0 \\
   \Rightarrow \left( {2x - 30} \right)\left( {x + 20} \right) = 0 \\
\]
\[ \Rightarrow 2x - 30 = 0\] or \[ \Rightarrow x + 20 = 0\]
\[
   \Rightarrow x = \dfrac{{30}}{2} \\
   = 15 \\
\] or \[ \Rightarrow x = - 20\]

Since the side of a right-angled triangle cannot be negative, we will discard \[x = - 20\].

Substituting this value of \[x\] in \[x + 5\], we get

\[15 + 5 = 20\]

Thus, the length of other sides of the triangle is 15 and 20 respectively.

Hence, option C is correct.

Note: In these types of questions, we will draw the diagram of a right-angled triangle for better understanding. In this question, first of all, note that the equation can also be factored using the quadratic formula to find the value of \[x\]. Also, some students end the question right after calculating the value of \[x\] and forget to find the other side.