Question

The hypotenuse of a right triangle is 25 cm, and the shorter leg is 15 cm. What is length of the other leg?

Answer 1

Hint: In a right- angled triangle the longest side is called hypotenuse, the side at the bottom is called base and the third side of the triangle is called the perpendicular.
 The relation between these sides of the right- angled triangle is given by
${\text{Hypotenus}}{{\text{e}}^{\text{2}}}{\text{ = Perpendicula}}{{\text{r}}^{\text{2}}}{\text{ + Bas}}{{\text{e}}^{\text{2}}}$
We’ll use this relation to find the length of other side.

Complete answer:
Given a right- angled triangle with length of hypotenuse $ = 25cm$ ,
Length of shorter side (say base of the triangle) $ = 15cm$ .
To find the length of the third side i.e., the perpendicular of the triangle.
The triangle becomes

For that we will use the relation ${\text{Hypotenus}}{{\text{e}}^{\text{2}}}{\text{ = Perpendicula}}{{\text{r}}^{\text{2}}}{\text{ + Bas}}{{\text{e}}^{\text{2}}}$ .
Putting the given lengths of the sides of the triangle, we get,
${\left( {25} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {15} \right)^2}$ ,
Now, taking ${\left( {15} \right)^2}$ on the left- hand side, we get,
${\left( {25} \right)^2} - {\left( {15} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2}$ ,
We know, ${\left( {25} \right)^2} = 625$ and ${\left( {15} \right)^2} = 225$ . Putting these values in above equation, we get,
\[625 - 225 = {\left( {{\text{Perpendicular}}} \right)^2}\] ,
On subtracting, we get, $400 = {\left( {{\text{Perpendicular}}} \right)^2}$ or ${\left( {{\text{Perpendicular}}} \right)^2} = 400$ .
Take square root on both sides, we get,
$\sqrt[2]{{{{\left( {{\text{Perpendicular}}} \right)}^2}}} = \sqrt[2]{{400}}$ i.e., Perpendicular ${\text{ = }}\sqrt[2]{{400}}$ .
Now, we’ll do prime factorisation of $400$ , which gives,
$400 = 2 \times 2 \times 2 \times 2 \times 5 \times 5$ .
Making pairs gives $400 = \underline {2 \times 2} \times \underline {2 \times 2} \times \underline {5 \times 5} $ .
So, $\sqrt {400} $ can be written as $\sqrt {400} = \sqrt {\underline {2 \times 2} \times \underline {2 \times 2} \times \underline {5 \times 5} } $ and these pairs will come out of the square root as one.
i.e., $\sqrt {400} = 2 \times 2 \times 5$ ,
so, $\sqrt {400} = 20$ .

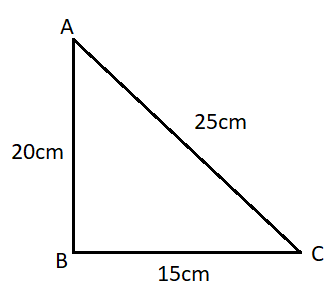
Hence, Perpendicular $ = 20cm$ i.e., the length of the other leg is $20cm$.

Note:
The relation used in this question between the hypotenuse, the perpendicular and the base is known as “Pythagoras Theorem”.
The Pythagoras Theorem is only valid for right- angled triangles.
While taking square roots, first do prime factorisation of the number then take the factors outside the root in pairs, as one and then multiply them.