Question

The horizontal distance between two trees of different height is $ 60m $ . The depression of the top of the first tree when seen from the top of the second tree is $ {45^0} $ . If the height of the second tree is $ 80m $ , find the length of the tree

Answer 1

Hint: To solve this problem, we will first understand the given conditions by drawing a representative diagram. Then we will use the principles of trigonometry to the right angle triangles formed. As the horizontal distance between two trees, angle of depression of the top of the first tree when seen from the top of the second tree and the height of the second tree is given, using tangent of the angle would be the best way to find our answer.

Complete step-by-step answer:
Our first step is to draw a representative diagram by the given data.

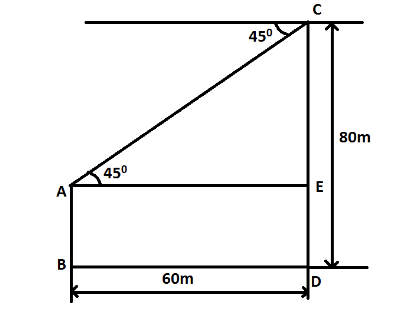
As shown in figure, AB and CD are the two trees. The horizontal distance BD and the height of the second tree CD is given and we are asked to find the length of the second tree AB.
From the diagram, it is clear that the length AB is equal to the length ED. For finding ED, we first need to find the length CE.
For this, let us consider the right angle triangle $ \vartriangle AEC $ in which $ \angle E $ is the right angle.
As per the diagram, $ \angle A = {45^0} $
Now, will take the tangent of this angle which is given as:
 $
  \tan A = \dfrac{{CE}}{{AE}} \\
   \Rightarrow CE = \tan A \times AE \;
  $
We know that $ \angle A = {45^0} \Rightarrow \tan A = \tan {45^0} = 1 $
Also, $ AE = BD = 60m $
 $ \Rightarrow CE = 1 \times 60 = 60m $
From the diagram,
 $
  CD = CE + ED \\
   \Rightarrow ED = CD - CE \;
  $
The length of the second tree is given as $ CD = 80m $ and we have determined $ CE = 60m $
 $ \Rightarrow ED = 80 - 60 = 20m $
It is visible from the diagram that
 $
  AB = ED \\
   \Rightarrow AB = 20\;m \;
  $
Thus, the length of the first tree is $ 20\;m $ .
So, the correct answer is “20 m”.

Note: In this type of question, it is always important to draw the representative diagram from the given data as it helps us to understand the relation between different dimensions. By this diagram, we need to identify a right angle triangle and then trigonometric functions to get the required dimensions. For example, here, we have used the tangent of $ \angle A $ in the right angle triangle $ \vartriangle AEC $ to get the length CE and then by the help of that we have determined our final answer.