Question

The horizontal distance between two trees of different height is 60m. The angle of depression of the top of the first tree when seen from the top of the second tree is ${45^0}$. If the height of the second tree is 80m, find the length of the tree.

Answer 1

Hint: In this question assume the unknown of the tree to be a variable, use the concept of trigonometric ratios to the respective triangles that can help in finding out the length of the smaller tree. It is advisable to use $\tan \theta $.

Complete step-by-step answer:

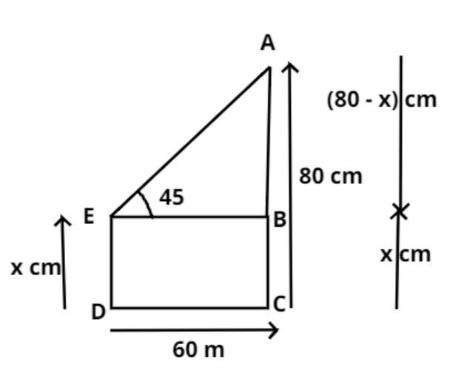
Let AC and ED be the two trees as shown in figure and the distance between two trees is 60 m as shown in figure.
$ \Rightarrow CD = 60$ meter.
So by symmetry EB = 60 meter (see figure).
Now it is given that the angle of depression of the top of the first tree when seen from the top of the second tree is 45 degrees as shown in figure.
$ \Rightarrow \angle AEB = {45^0}$
Now it is given that the height of the second tree is 80 meter.
Therefore AC = 80 meter (see figure).
Let the length of the first tree be x meter.
Therefore ED = x meter.
So by symmetry BC = x meter (see figure).
As from the figure
$AC = AB + BC$
So substitute the values in the above equation we have,
$ \Rightarrow 80 = AB + x$
$ \Rightarrow AB = 80 - x$ meter (see figure).
Now in triangle AEB
$ \Rightarrow \tan {45^0} = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \dfrac{{AB}}{{EB}} = \dfrac{{80 - x}}{{60}}$
$ \Rightarrow 1 = \dfrac{{80 - x}}{{60}}$
Now simplify the above equation we have,
$ \Rightarrow 60 = 80 - x$
$ \Rightarrow x = 80 - 60 = 20$ meter.
So the length of the first tree is 20 meter.

Note: Whenever we face such types of problems the key concept is to build the diagrammatic representation using the information provided in the question, as it helps figuring out the respective triangles which will get us to the required quantity. The direct formula for the trigonometric ratios also need to be remembered.