
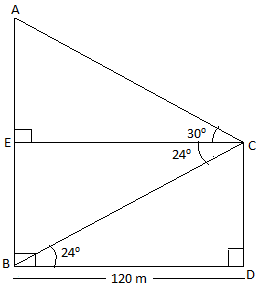
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is \[{{30}^{\circ }}\] and \[{{24}^{\circ }}\] respectively. Find the height of the two towers. Give your answer correct to 4 significant figures.

Answer
612.9k+ views
Hint: For the given question, we will consider the \[\Delta BCD\] from the given figure and we will use the tangent of \[\angle CBD\] which will give us the value of CD. Again, we will consider \[\Delta AEC\] and we will use the tangent of \[\angle ACE\] which will give us the value of AE.
Complete step-by-step answer:
We have been given the distance between two towers is 120 m and the angle of elevation of top and angle of depression of the bottom of first tower as observed from the second tower is \[{{30}^{\circ }}\] and \[{{24}^{\circ }}\] respective which are shown in the figure as follows:
Now in \[\Delta BCD\], we have \[\angle CBD={{24}^{\circ }}\] and BD = 120 m. Since it is a right angled triangle, we can find \[\tan \theta =\dfrac{perpendicular}{base}\].
\[\begin{align}
& \tan {{24}^{\circ }}=\dfrac{CD}{BD} \\
& \tan {{24}^{\circ }}=\dfrac{CD}{120} \\
& CD=120\times \tan {{24}^{\circ }} \\
\end{align}\]
As we know that the approximate value of \[\tan {{24}^{\circ }}=0.4452\]
\[\begin{align}
& CD=120\times 0.4452 \\
& CD=53.42m \\
\end{align}\]
Once again, in \[\Delta AEC\] we have EC = BD = 120 m and \[\angle ACE={{30}^{\circ }}\].
Since it is a right angled triangle we can find \[\tan \theta =\dfrac{perpendicular}{base}\].
\[\begin{align}
& \tan {{30}^{\circ }}=\dfrac{AE}{EC} \\
& \tan {{30}^{\circ }}=\dfrac{AE}{120} \\
& AE=120\times \tan {{30}^{\circ }} \\
\end{align}\]
As we know that the approximate value of \[\tan {{30}^{\circ }}=0.577\].
\[\begin{align}
& AE=120\times 0.577 \\
& AE=69.24m \\
\end{align}\]
Also, we know that AB = AE + BE and BE = CD.
\[AB=AE+CD=69.24+53.42=122.66m\]
We can also write it as \[122.7m\]
Therefore, the height of the towers are 53.42 m and 122.7 m approximately correct upto 4 significant figures.
Note: Be careful while substituting the values of tangent in the equation as there is a chance of multiplication error.
We can also solve the above question if we consider the other triangles from the figure.
Also, take care of the significant figures of your final answer.
Complete step-by-step answer:
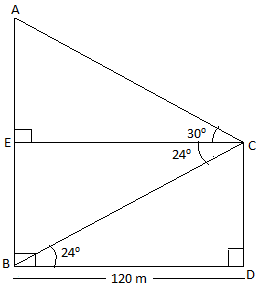
We have been given the distance between two towers is 120 m and the angle of elevation of top and angle of depression of the bottom of first tower as observed from the second tower is \[{{30}^{\circ }}\] and \[{{24}^{\circ }}\] respective which are shown in the figure as follows:

Now in \[\Delta BCD\], we have \[\angle CBD={{24}^{\circ }}\] and BD = 120 m. Since it is a right angled triangle, we can find \[\tan \theta =\dfrac{perpendicular}{base}\].
\[\begin{align}
& \tan {{24}^{\circ }}=\dfrac{CD}{BD} \\
& \tan {{24}^{\circ }}=\dfrac{CD}{120} \\
& CD=120\times \tan {{24}^{\circ }} \\
\end{align}\]
As we know that the approximate value of \[\tan {{24}^{\circ }}=0.4452\]
\[\begin{align}
& CD=120\times 0.4452 \\
& CD=53.42m \\
\end{align}\]
Once again, in \[\Delta AEC\] we have EC = BD = 120 m and \[\angle ACE={{30}^{\circ }}\].
Since it is a right angled triangle we can find \[\tan \theta =\dfrac{perpendicular}{base}\].
\[\begin{align}
& \tan {{30}^{\circ }}=\dfrac{AE}{EC} \\
& \tan {{30}^{\circ }}=\dfrac{AE}{120} \\
& AE=120\times \tan {{30}^{\circ }} \\
\end{align}\]
As we know that the approximate value of \[\tan {{30}^{\circ }}=0.577\].
\[\begin{align}
& AE=120\times 0.577 \\
& AE=69.24m \\
\end{align}\]
Also, we know that AB = AE + BE and BE = CD.
\[AB=AE+CD=69.24+53.42=122.66m\]
We can also write it as \[122.7m\]
Therefore, the height of the towers are 53.42 m and 122.7 m approximately correct upto 4 significant figures.
Note: Be careful while substituting the values of tangent in the equation as there is a chance of multiplication error.
We can also solve the above question if we consider the other triangles from the figure.
Also, take care of the significant figures of your final answer.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




