Question

The hemispherical dome of a building needs to be painted. If the circumference of the base of the dome is 17.6 m, find the cost of painting it, given the cost of painting is Rs 5 per 100 ${\text{c}}{{\text{m}}^2}$.

Answer 1

Hint- Here, we will proceed by using the formula for the circumference of any circle of radius r which is given by $2\pi r$ and from here we will find the value of radius of the base of the hemispherical dome and then we will use the formula i.e., curved surface area of a hemisphere with base radius r = $2\pi {r^2}$.

Complete step-by-step answer:

Given, Circumference of the base of dome = 17.6 m
Cost of painting 100 ${\text{c}}{{\text{m}}^2}$ = Rs 5
As we know that 1 ${{\text{m}}^2}$ = 10000 ${\text{c}}{{\text{m}}^2}$
$
   \Rightarrow {\text{1 c}}{{\text{m}}^2} = \dfrac{1}{{10000}}{\text{ }}{{\text{m}}^2} \\
   \Rightarrow {\text{100 c}}{{\text{m}}^2} = \left( {100} \right)\left( {\dfrac{1}{{10000}}} \right){\text{ }}{{\text{m}}^2} \\
   \Rightarrow {\text{100 c}}{{\text{m}}^2} = \dfrac{1}{{100}}{\text{ }}{{\text{m}}^2} \\
 $
So, Cost of painting $\dfrac{1}{{100}}{\text{ }}{{\text{m}}^2}$ = Rs 5
$ \Rightarrow $Cost of painting $1{\text{ }}{{\text{m}}^2}$ = Rs $\left( {5 \times 100} \right)$ = Rs 500
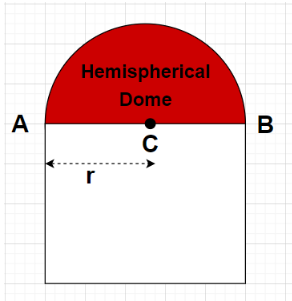
Let r be the radius of the base of the hemispherical dome as shown in the figure
Also, circumference of any circular surface having radius r = $2\pi r$ where $\pi = \dfrac{{22}}{7}$
Circumference of the base of dome = $2\pi r$
$
   \Rightarrow 17.6 = 2\pi r \\
   \Rightarrow r = \dfrac{{17.6}}{{2\pi }} = \dfrac{{17.6}}{{2\left( {\dfrac{{22}}{7}} \right)}} = \dfrac{{17.6 \times 7}}{{44}} \\
   \Rightarrow r = 2.8{\text{ m}} \\
 $
So, the radius of the base of the hemispherical dome is 2.8 m
It is given that only the hemispherical dome in the building coloured red in the figure needs to be painted which means only the curved surface area of the hemispherical dome will be painted.
Since, Curved surface area of a hemisphere with base radius r = $2\pi {r^2}$
Curved surface area of the hemispherical dome painted (red colour in figure) = $2\left( {\dfrac{{22}}{7}} \right){\left( {2.8} \right)^2}$
$ \Rightarrow $ Curved surface area of the hemispherical dome painted (red colour in figure) = 49.28 ${{\text{m}}^2}$
Also, Total cost of painting the hemispherical dome = (Cost of painting $1{\text{ }}{{\text{m}}^2}$)$ \times $( Curved surface area of the hemispherical dome painted in ${{\text{m}}^2}$)
$ \Rightarrow $Total cost of painting the hemispherical dome = $500 \times 49.28 = {\text{Rs }}24640$
Therefore, the total cost of painting the hemispherical dome of a building is Rs 24640.

Note- In this particular problem, the base of the hemispherical dome is open and is not painted that’s why only the curved surface of the hemisphere is painted. Also, the base of the hemisphere is always a circular surface. Here, it is important to make sure that the units are identical. Here, we have converted every unit into ${{\text{m}}^2}$.