Question

The height up to which water will rise in a capillary tube will be:
A. Maximum when water temperature is $4^{\circ}C$
B. Minimum when water temperature is $4^{\circ}C$
C. Minimum when water temperature is $0^{\circ} C$
D. Same at all temperatures

Answer 1

Hint: We know that when a capillary tube is wet by the water in a trough, the water molecules adhere to the sides of the tube and rise upwards to a certain height. The upward reaction force is brought about by components of surface tension acting tangential to the water meniscus and this is balanced out by the weight of the water in the capillary tube. Evaluate this balance at equilibrium to arrive at an expression relating height of the water to density of water at $0^{\circ}C$ and $4^{\circ}C$.

Formula used:
Height of ascent $ h = \dfrac{2T\cos\theta}{r\rho g}$

Complete step-by-step answer:
Consider a capillary tube of uniform width that is dipped into a trough containing water such that it wets the tube. Since the water wets the inner sides of the tube and it adhesively rises through the walls of the tube, it forms a concave meniscus as shown in the diagram. Thus, the surface tension$\;T$ acts inwards along the tangents to the meniscus as shown.
Let the radius of the tube be$\;r$ and let $\theta$ be the angle of contact between the liquid and the glass. The surface tension can be resolved into its horizontal and vertical components.
Now, the surface tension is usually defined as force per unit length, and this force is equivalent to the reaction force, say,$\;N$ acting on the meniscus, i.e.,
$T = \dfrac{N}{l} \Rightarrow N = T \times l$
This reaction force is responsible for raising the water through the tube. Since the component of the surface tension contributing towards raising the water through the tube is $T\cos\theta$ that acts along the sides of the tube throughout the entire circumference of the tube, the reaction force can be given as:
$N = T \times l = T\cos\theta \times 2\pi r = 2\pi rT\cos\theta$

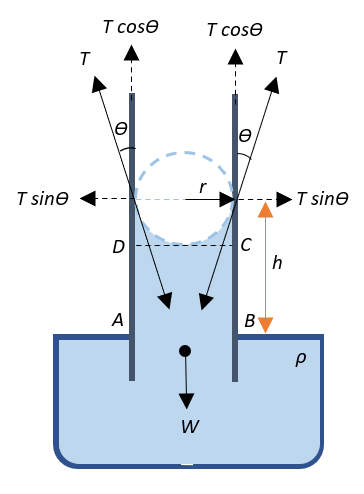
Now, water in the tube is contained cylindrically. Therefore, the volume of water in the tube if the water rises to a height $\;h$ can be given by:
$V = \pi r^2 h$
If the density of water is $\rho$, then the mass of water in the tube can be given by:
$m = V \times \rho = \pi r^2 h \rho$
Therefore, the weight of the water in the tube will be:
$W = mg = \pi r^2 h\rho g$
Now, in equilibrium, the weight of the water in the tube is balanced by the normal reaction force acting on it, i.e.,
$W = N$
$\Rightarrow \pi r^2 h\rho g = 2\pi rT\cos\theta $
$\Rightarrow h = \dfrac{2T\cos\theta}{r\rho g}$
Now, we know that the density of water is maximum at $4^{\circ}C$ and minimum at $0^{\circ}C$ due to the anomalous expansion of water as it goes from $4^{\circ}C$ to $0^{\circ}C$. From the above equation, we can establish that:
$h \propto \dfrac{1}{\rho}$
Thus, if the density of water is maximum at $4^{\circ}C$, then the height to which the water in the capillary tube will rise will be minimum.
Therefore, the correct choice would be B. Minimum when water temperature is $4^{\circ}C$

So, the correct answer is “Option B”.

Note: It is important to understand why water has maximum density at $4^{\circ}C$. In the form of iceat $0^{\circ}C$, water molecules are arranged in a crystal lattice that encompasses a lot of empty space, decreasing the density. Now, as the ice begins to melt into liquid water, the crystal ice structure collapses and the water molecules are free to move closer to each other up until $4^{\circ}C$, thereby increasing the density. Beyond this temperature, the water molecules begin to move further apart, gradually decreasing the density again. This is why, optimally at $4^{\circ}C$, water has maximum density.