Question

The height of water in a vessel is $ h $ . The vessel wall of width $ b $ is at an angle $ \theta $ to the vertical. The net force exerted by the water on the wall is:

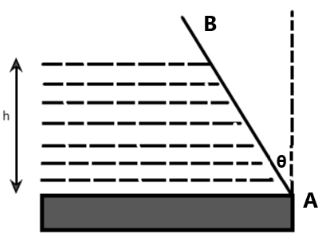
(A) $ \dfrac{1}{2}\rho b{h^2}g\cos \theta $
(B) $ \dfrac{1}{2}\rho b{h^2}g $
(C) $ \dfrac{1}{2}\rho b{h^2}g\sec \theta $
(D) Zero

Answer 1

Hint : The length of the wall in contact with the water when it is bent is longer than the length if it had not been at angle to the vertical. So we can find the force from the formula, $ F = PA $ where we have to substitute the average pressure and the area will be the area that is in contact with the fluid.

Formula used: In this solution we will be using the following formula;
 $ F = PA $ where $ P $ is the pressure on a surface, $ F $ is the force exerted on that surface, and $ A $ is the area of the surface.
 $ P = \rho gh $ where $ P $ is the pressure at a particular point in a fluid, $ \rho $ is the density of the fluid, and $ g $ is acceleration due to gravity, and $ h $ is the depth from the free surface of the liquid.

Complete step by step answer:

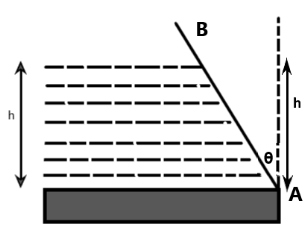
Observe that the length of the wall in contact with the water is higher at an angle to the vertical than if it were exactly vertical. From diagram, we see that
 $ h = l\cos \theta $
hence,
 $ l = \dfrac{h}{{\cos \theta }} = h\sec \theta $
Now, the pressure of liquid at a particular depth below the surface is given as
 $ P = \rho gh $ where $ P $ is the pressure at a particular point in a fluid, $ \rho $ is the density of the fluid, and $ g $ is acceleration due to gravity, and $ h $ is the depth from the free surface of the liquid.
However, in such a vessel, the average pressure act at $ \dfrac{h}{2} $ of the vessel, hence the average pressure on the surface is given as
 $ {P_{ave}} = \rho g\dfrac{h}{2} $
Hence, the net force is
 $ {F_{ave}} = {F_{NET}} = {P_{ave}}A $
The area in contact with the fluid is given as
 $ A = lb $ where $ l $ is the total length, and $ b $ is the width.
But $ l = h\sec \theta $ hence,
 $ A = bh\sec \theta $
Then $ {F_{ave}} = \rho g\dfrac{h}{2}bh\sec \theta $
 $ \Rightarrow {F_{ave}} = \dfrac{1}{2}\rho b{h^2}g\sec \theta $
Hence, the correct option is C.

Note:
For clarity, the position of the average pressure can be proven from
 $ {P_{ave}} = \dfrac{1}{A}\int_0^h {PdA} = \dfrac{1}{A}\int_0^h {\rho ghdA} $ as follows
In this case,
 $ dA = bdl $ since width is the same and we are gradually moving up along the length.
But $ l = h\sec \theta $
 $ \Rightarrow dl = dh\sec \theta $
Hence,
By inserting $ dA = bdh\sec \theta $ into $ \dfrac{1}{A}\int_0^h {\rho ghdA} $ we have
 $ {P_{ave}} = \dfrac{1}{{bh\sec \theta }}\int_0^h {\rho ghbdh\sec \theta } $
 $ \Rightarrow {P_{ave}} = \dfrac{1}{{bh\sec \theta }}\rho g\dfrac{{{h^2}}}{2}b\sec \theta $
Then, by cancelations,
 $ {P_{ave}} = \rho g\dfrac{h}{2} $
Which implies that the average pressure acts at depth or height $ \dfrac{h}{2} $ (exactly at the middle of the vessel).