Question

The height of the right circular cylinder is 5 and the diameter of its base is 4. What is the distance from the centre of one base to a point on the circumference of the other base?
A) 3
B) 5
C) $\sqrt{29}$
D) $\sqrt{33.}$

Answer 1

Hint: In order to solve this question, where we have been asked for the distance from the centre of one base to a point on the circumference of other bases, we need to follow the Pythagoras theorem to get to our result.

Complete step by step solution: It is given that;
The height of the right circular cylinder is $\left( h \right)=5;$
And, the diameter of its base $=4.$
radius of its base $\left( r \right)=\dfrac{1}{2}\times $ diameter of its base $=\dfrac{1}{2}\times 4=2$.
Let the distance from the centre of one base to the point on the circumference of other base be ‘l’ we observe that;
(height of the cylinder), (radius of the cylinder) and (the line joining the centre of one base to the point on the circumference of another base) from a right-angled triangle with a hypotenuse of length ‘l’.
To find the value of ‘l’, we need to follow the Pythagoras theorem:-
By Pythagoras theorem :

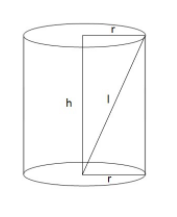
${{l}^{2}}={{h}^{2}}+{{r}^{2}}$
$\Rightarrow {{l}^{2}}={{\left( 5 \right)}^{2}}+{{\left( 2 \right)}^{2}}$
$\Rightarrow {{l}^{2}}=25+4$
$\Rightarrow {{l}^{2}}=29$
$\Rightarrow l=\sqrt{29}$
$\Rightarrow $
Therefore, distance from the centre of one base to a point on the circumference of the other base is $ \sqrt{29}.$

Hence, Option (C) is the correct answer to this question.

Note: Note :
In a right circular cylinder, the axis of the cylinder is perpendicular to the base of the cylinder while in a normal cylinder, it is a parallelogram.
The cross-section of a right circular cylinder is a circle, and the axis of the cylinder is perpendicular to the base.
Pythagoras theorem : ${{\left( \text{hypotenuse} \right)}^{\text{2}}}\text{=}{{\left( \text{height} \right)}^{\text{2}}}\text{+}{{\left( \text{base} \right)}^{\text{2}}}$