Question

The height of an equilateral triangle is 10 cm. Its area is.

(a) $\dfrac{100}{3}\text{ c}{{\text{m}}^{2}}$
(b) $30\text{ c}{{\text{m}}^{2}}$
(c) $100\text{ c}{{\text{m}}^{2}}$
(d) $\dfrac{100}{\sqrt{3}}\text{ c}{{\text{m}}^{2}}$

Answer 1

Hint: For solving this question firstly we will draw the figure of the given equilateral triangle and try to find the length of the base QR of the triangle by applying some basic concepts of trigonometry like $\sin \theta =\dfrac{\text{length of the perpendicular}}{\text{length of the hypotenuse}}$ . After that, we will find the value of the area by applying the formula $\dfrac{1}{2}\times \left( base \right)\times \left( height \right)$ correctly.

Complete step-by-step solution -
Given:
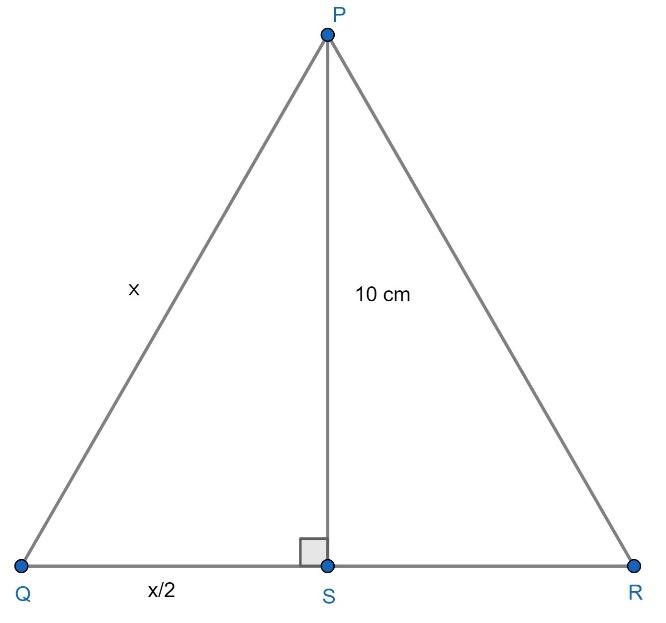
We have an equilateral triangle with height PQ of 10 cm, and we have to find the value of the area of the given equilateral triangle.
Now, let there is an equilateral triangle PQR with side $x$ cm, and PS is the perpendicular drawn from the vertex P to the side QR and as it is an equilateral triangle PS will bisect the side QR. Moreover, as it is an equilateral triangle, the value of $\angle PQR=\angle QPR=\angle QRP={{60}^{0}}$ . For more clarity look at the figure given below:

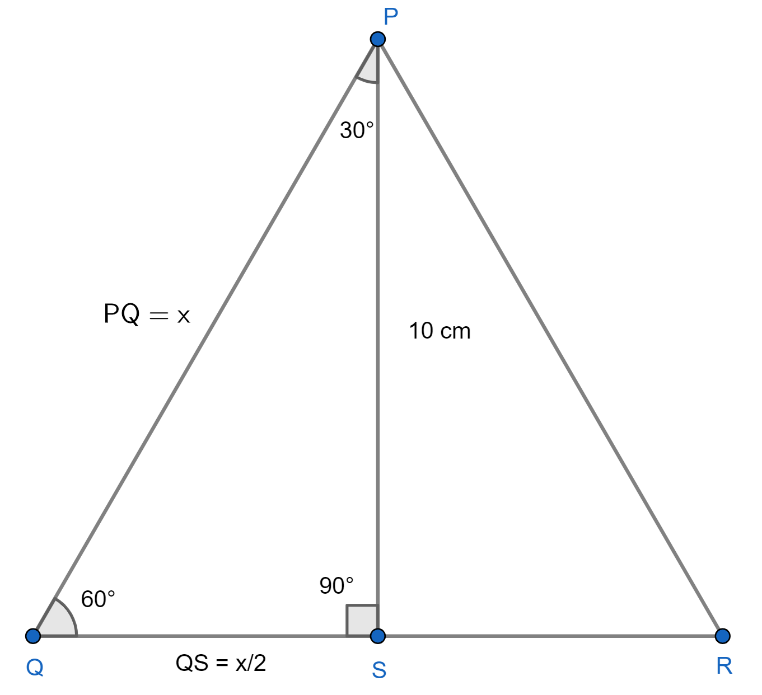
In the above figure, as PS bisects QR so, length of QS will be equal to $\dfrac{x}{2}$ cm.
Now, consider $\Delta PQS$ we have $PQ=x,PS=10$ and $\angle PQS={{60}^{0}},\angle PSQ={{90}^{0}}$ . Then,
$\begin{align}
  & \sin \left( \angle PQS \right)=\dfrac{\left( \text{lenght of the perpendicular PS} \right)}{\left( \text{length of the hypotenuse PQ} \right)} \\
 & \Rightarrow \sin {{60}^{0}}=\dfrac{PS}{PQ} \\
 & \Rightarrow PQ\times \dfrac{\sqrt{3}}{2}=PS \\
 & \Rightarrow PQ=\dfrac{10}{\sqrt{3}}\times 2 \\
 & \Rightarrow x=\dfrac{20}{\sqrt{3}}\text{ cm} \\
\end{align}$
Now, in the equilateral triangle, PQR we have the length of the base QR equal to $\dfrac{20}{\sqrt{3}}$ cm and length of the height PS is equal to 10 cm. Then,
$\begin{align}
  & Area=\dfrac{1}{2}\times \left( base \right)\times \left( height \right) \\
 & \Rightarrow Area=\dfrac{1}{2}\times \dfrac{20}{\sqrt{3}}\times 10 \\
 & \Rightarrow Area=\dfrac{100}{\sqrt{3}}\text{ c}{{\text{m}}^{2}} \\
\end{align}$
Now, from the above result, we conclude that the value of the area of the given equilateral triangle will be $\dfrac{100}{\sqrt{3}}\text{ c}{{\text{m}}^{2}}$ .
Hence, (d) is the correct option.

Note: Here, the student should first understand the basic concepts of the equilateral triangle and then apply the basic concept of trigonometry. After that, find the base QR of the triangle and then calculate the value of the area of the triangle by the conventional formula. Moreover, for objective problems, we could use directly formula $\dfrac{\sqrt{3}}{4}{{a}^{2}}$ to find the area of an equilateral triangle of side $a$ units.