Question

The height of a tower is ‘h’ and α is the angle of elevation of the top of the tower. On moving a distance $\dfrac{h}{2}$ towards the tower, the angle of elevation becomes β. What is the value of $\cot \alpha - \cot \beta $?
A. $\dfrac{1}{2}$
B. $\dfrac{2}{3}$
C. 1
D. 2

Answer 1

Hint: Given the height of the tower is h and the angle of elevation is α. When we move a distance of $\dfrac{h}{2}$ towards the tower the angle of elevation becomes β. The tower is perpendicular to the ground so it makes a right triangle. Find the value of cot α in terms of h, x and also cot β in terms of h and x and solve for its value. The result must be in terms of either h or a constant.

Complete step-by-step answer:

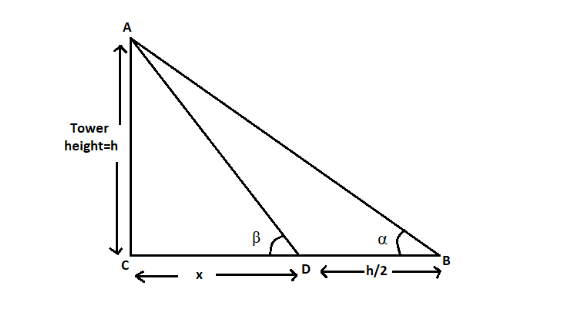
We are given that the height of a tower is ‘h’ and α is the angle of elevation of the top of the tower. On moving a distance $\dfrac{h}{2}$ towards the tower, the angle of elevation becomes β.
We have to find the value of $\cot \alpha - \cot \beta $
As we can see in the diagram, triangles ABC and ADC are right triangles with hypotenuses AB and AD respectively.
The function Cot (cotangent) of angle x is the ratio of the adjacent side to angle x and opposite side to angle x.
Therefore, in triangle ABC
 $
  \cot \alpha = \dfrac{{CB}}{{AC}} = \dfrac{{CD + DB}}{{AC}} \\
  CB = x + \dfrac{h}{2},AC = h \\
   \to \cot \alpha = \dfrac{{\left( {x + \dfrac{h}{2}} \right)}}{h} \\
   \to h\cot \alpha = x + \dfrac{h}{2} \\
  \therefore x = h\cot \alpha - \dfrac{h}{2} \to eq(1) \\
 $
In triangle ADC,
$
  \cot \beta = \dfrac{{CD}}{{AC}} \\
  CD = x,AC = h \\
   \to \cot \beta = \dfrac{x}{h} \\
  \therefore x = h\cot \beta \to eq(2) \\
 $
Subtracting equations 1 and 2, we get
$
  0 = \left( {h\cot \alpha - \dfrac{h}{2}} \right) - \left( {h\cot \beta } \right) \\
   \to h\cot \alpha - \dfrac{h}{2} - h\cot \beta = 0 \\
   \to h\left( {\cot \alpha - \cot \beta } \right) - \dfrac{h}{2} = 0 \\
   \to h\left( {\cot \alpha - \cot \beta } \right) = \dfrac{h}{2} \\
  \therefore \cot \alpha - \cot \beta = \dfrac{1}{2} \\
 $
The value of $\cot \alpha - \cot \beta $ is $\dfrac{1}{2}$
Therefore, the correct option is Option A, $\dfrac{1}{2}$
So, the correct answer is “Option A”.

Note: An alternate way to find the value of cot.
Function Sine of x is the ratio of its opposite side and hypotenuse. Function Cosine of x is the ratio of its adjacent side and hypotenuse.
Tangent function is the ratio of the above sine and cosine functions.
And the cot (cotangent) function is the reciprocal of the above tangent function or the ratio of cosine and sine functions. Thus we can find the value of cot using sine and cosines instead of directly using its definition.