Question

The height of a tower is 50 metre. When the sun’s altitude increases from 30° to 45°. The length of the shadow of the tower is decreased by x metre. Find the approximate value of x in metres.
A.86.6
B.36.6
C.50
D.None of these

Answer 1

Hint: First of all, we will draw the figure and then we will use the trigonometric identity: tan $\theta $ = $\dfrac{{perpendicular}}{{base}}$ in then obtained triangles. We will use this identity twice and using the equation (1) while using the tan 45° into the equation using tan 30°, we will calculate the value of the decrease in shadow of the tower (i.e., the value of x) in metres.

Complete step-by-step answer:
 We are given a tower whose height is 50 metres.
It is said that when the altitude of the sun changes from 30° to 45°, the length of the shadow of the tower gets shortened by x metres. We are required to calculate the value of x (in metres).
For this, let us draw the figure of this setup:

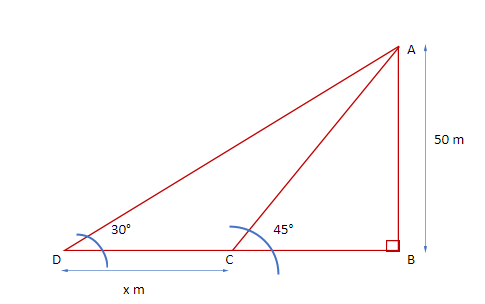
From the figure, we can say that in the right angled triangle ABC,
Using the trigonometric formula: tan $\theta $ = $\dfrac{{perpendicular}}{{base}}$, we get
$ \Rightarrow $ tan 45° = $\dfrac{{AB}}{{BC}}$
$ \Rightarrow $ 1 = $\dfrac{{50}}{{BC}}$
$ \Rightarrow $BC = 50 metres – equation (1)
Now, in the right angled triangle ABD,
Using the trigonometric formula: tan $\theta $ = $\dfrac{{perpendicular}}{{base}}$, we get
$ \Rightarrow $tan 30° = $\dfrac{{AB}}{{BD}}$
$ \Rightarrow $tan 30° = $\dfrac{{50}}{{DC + BC}}$
$ \Rightarrow $$\dfrac{1}{{\sqrt 3 }}$ = $\dfrac{{50}}{{DC + 50}}$
$
   \Rightarrow DC + 50 = 50\sqrt 3 \\
   \Rightarrow DC = 50\sqrt 3 - 50 \\
   \Rightarrow x = 50\left( {\sqrt 3 - 1} \right) \\
   \Rightarrow x = 50\left( {1.732 - 1} \right) \\
   \Rightarrow x = 50\left( {0.732} \right) \\
   \Rightarrow x = 36.6 \\
 $ using ($\sqrt 3 $ = 1.732)
Therefore, the length of the shadow of the tower is 36.6 metres.
Hence, option (B) is correct.

Note: In this question, you may go wrong while sketching the diagram from the given word problem especially the part of length of shadow. Be careful while calculating for the value of x by using the trigonometric identities since you need to use tan$\theta $ twice for solving the value of x.