Question

The height of a right circular cylinder of maximum volume inscribed in a sphere of radius $3$ is
(a) $2\sqrt{3}$
(b) $\sqrt{3}$
(c) $\sqrt{6}$
(d) $\dfrac{2}{3}\sqrt{3}$

Answer 1

Hint: So here in this question we will use the formula of the Volume of the cylinder, which is $V=\pi {{r}^{2}}h$. and we will Use the condition of maxima and minima to solve this question. For this we have to use the $\sin \theta \,\,\And \,\,\cos \theta $ formula with the help of these we will find the value of h. and then after finding h we have to find the value of V then after to find maximum height we have to find the maximum volume for that we have to double derivate V. then we will get the value of h which is the maximum height of the cylinder.

Complete step by step answer:

Let us try to understand this by drawing a figure of the right circular cylinder inscribed in a sphere.

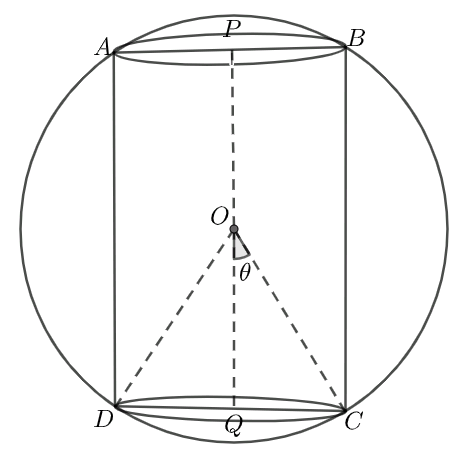
We will represent $R$ as radius of sphere and $r$ as the radius of the cylinder. Let us consider $h$ as the height of the cylinder. Let us consider $\angle QOC=\theta $ . Then in $\Delta QOC$ , we have
 $\dfrac{QC}{OC}=\sin \theta $
As \[O\] is centre of cylinder and sphere, therefore \[OC\] is the radius of sphere.
 \[\therefore OC=3\]
Also \[QC\] is radius of cylinder therefore \[QC=r\] .
 $\begin{align}
  & \therefore \dfrac{r}{3}=\sin \theta \\
 & \Rightarrow r=3\sin \theta \\
\end{align}$
Similarly, $\dfrac{OQ}{OC}=\cos \theta $
We have $OQ=\dfrac{h}{2}=half\text{ }of\text{ }the\text{ }height\text{ }of\text{ }the\text{ }cylinder$
 $\begin{align}
  & \therefore \dfrac{\dfrac{h}{2}}{3}=\cos \theta \\
 & \Rightarrow \dfrac{h}{6}=\cos \theta \\
 & \Rightarrow h=6\cos \theta ...............\left( 1 \right) \\
\end{align}$
Now , we know that volume of a cylinder of height $'h'$ and radius $'r'$ is
$V=\pi {{r}^{2}}h$
 \[\begin{align}
  & \therefore V=\pi \times {{\left( 3\sin \theta \right)}^{2}}\times 6\cos \theta \\
 & \Rightarrow V=\pi \times 9{{\sin }^{2}}\theta \times 6\cos \theta \\
 & \Rightarrow V=54\pi si{{n}^{2}}\theta \cos \theta \\
 & \Rightarrow V=54\pi \left( 1-{{\cos }^{2}}\theta \right)\cos \theta \\
 & \Rightarrow V=54\pi \left( \cos \theta -{{\cos }^{3}}\theta \right) \\
\end{align}\]
Now, let us differentiate $V$ w.r.t $\theta $ ,
 \[\therefore \dfrac{dV}{d\theta }=54\pi \left[ \left( -\sin \theta -(-3{{\cos }^{2}}\theta .\sin \theta \right) \right]\]
Now, put $\dfrac{dV}{d\theta }=0$
i.e., $54\pi \left( -\sin \theta +3{{\cos }^{2}}\theta .\sin \theta \right)=0$
It means either $\sin \theta =0$ or $\cos \theta =\dfrac{1}{\sqrt{3}}$
Now, let us find $\dfrac{{{d}^{2}}V}{d{{\theta }^{2}}}$ .
 \[\begin{align}
  & \therefore \dfrac{{{d}^{2}}V}{d{{\theta }^{2}}}=54\pi \left[ -\cos \theta +3\left\{ \sin \theta .2\cos \theta \left( -\sin \theta \right)+{{\cos }^{2}}\theta .\cos \theta \right\} \right] \\
 & \text{ =}-54\pi \left[ \cos \theta +6\sin \theta .\cos \theta +{{\cos }^{3}}\theta \right] \\
\end{align}\]
which is negative.
 $\therefore $ Volume is maximum.
Now we can take $\cos \theta =\dfrac{1}{\sqrt{3}}$
 $\therefore $ From $\left( 1 \right)$
 $h=6\cos \theta =6\times \dfrac{1}{\sqrt{3}}=6\times \dfrac{1}{\sqrt{3}}\times \dfrac{\sqrt{3}}{\sqrt{3}}=6\times \dfrac{\sqrt{3}}{3}=2\sqrt{3}$
 $\therefore $ Height of the cylinder is $2\sqrt{3}$ .
Hence the correct option is (a).
Note: For this type of questions firstly we have to find the maximum volume of the cylinder then we only we will get the maximum height if we find the volume and then we will find the then our answer will be wrong for that we have to double derivate the V then we will get the value of maximum height. So take care of it first find the maximum volume then we will get the maximum height.