Question

The height of a light house is 85m. An observer on it found the angle of depression to a boat to be 30 degree, which was sailing towards the light house. After two minutes, the angle of depression for the same boat was 60degree. What was the speed of the boat in km/hr?

Answer 1

Hint: In this question, the angle of depression of the boat at two points are given. We can thus find the distance of the boat from the base of the lighthouse by using standard trigonometric formulas. Then, we can subtract the distance of the boats from the lighthouse at the two instances to obtain the distance travelled by the boat in the time which is given in the question. Thus, by knowing the distance covered and time taken, we can find the speed of the boat by using the definition of speed.

Complete step-by-step solution -
The situation can be represented by the figure below.

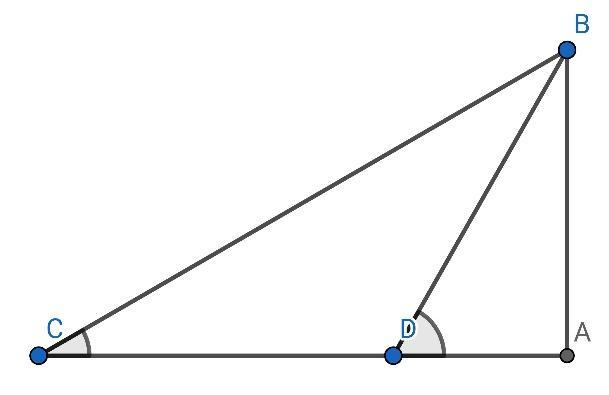
Here, AB represents the lighthouse of height 85m and C and D are the positions of the boat initially and 2minutes later respectively. It is given that \[\angle BCD={{30}^{\circ }}\] and \[\angle BDA={{60}^{\circ }}\]…………………….(1.1)
In a right angled triangle, the tangent of an angle theta is given by
$\text{tangent of }\theta \text{=}\tan (\theta )=\dfrac{\text{length of the side opposite to the angle }\theta }{\text{length of the side adjacent to the angle }\theta }...................(1.2)$
Also, from trigonometry we know that $\tan ({{60}^{\circ }})=\sqrt{3}$ and $\tan ({{30}^{\circ }})=\dfrac{1}{\sqrt{3}}$……………………….(1.3)
We are given that the height of the lighthouse (AB) is 85m. Therefore, using equation (1.2) in $\Delta BCA$ , we obtain
$\begin{align}
  & \tan \left( \angle BCA \right)=\dfrac{AB}{AC} \\
 & \Rightarrow \tan ({{30}^{\circ }})=\dfrac{85m}{AC}\text{ (using the information in 1}\text{.1)} \\
 & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{85m}{AC}(\text{using (1}\text{.3)}) \\
 & \Rightarrow AC=85\sqrt{3}m..................(1.4) \\
\end{align}$
After two minutes, the position of the boat would be at point D. Therefore, using equation (1.2), we obtain
\[\begin{align}
  & \tan \left( \angle BDA \right)=\dfrac{AB}{AD} \\
 & \Rightarrow \tan ({{30}^{\circ }})=\dfrac{85m}{AD}\text{ (using the information in 1}\text{.1)} \\
 & \Rightarrow \sqrt{3}=\dfrac{85m}{AD}(\text{using (1}\text{.3)}) \\
 & \Rightarrow AD=\dfrac{85}{\sqrt{3}}m..................(1.4) \\
\end{align}\]
Thus, the distance travelled by the boat in two minutes will be equal to
$\text{Distance Travelled by boat=AC-AD=85}\sqrt{3}m-\dfrac{85}{\sqrt{3}}m=\dfrac{1}{1000}\times \left( \text{85}\sqrt{3}m-\dfrac{85}{\sqrt{3}} \right)km\text{ (as 1km=1000m)}.............(1.5)$
The formula for finding the speed from the distance covered and time taken is
$Speed=\dfrac{\text{Distance Travelled}}{\text{Time Taken}}...........(1.6)$
In this case, the time taken is
\[2mins=\dfrac{2}{60}hours\text{ }(\text{as 1hour=60minutes}).........(1.7)\]
Thus, by using equations (1.5), (1.6) and (1.7), we find that the speed of the boat is
$Speed=\dfrac{\dfrac{1}{1000}\left( 85\sqrt{3}-\dfrac{85}{\sqrt{3}} \right)km}{\dfrac{2}{60}hr}=2.94km/hr$
Thus, the speed of the boat is found to be 2.94km/hr.

Note: We must convert the time taken by the boat to travel from C to D in hour units and the distance to km units as in the question, the speed is asked to be found out in km/hr.