
The harmonic mean of the segments of a focal chord of \[{{y}^{2}}=8x\] .
A. 16
B. 5
C. 8
D. 4
Answer
610.5k+ views
Hint: By comparing \[{{y}^{2}}=8x\] and general equation of parabola ${{y}^{2}}=4ax$ , find the value of a. the harmonic mean of 2 no: x & y is of the form $\dfrac{2}{\dfrac{1}{x}+\dfrac{1}{y}}$ . The coordinate of A & B of focal chord are of the form $\left( a{{t}^{2}},2at \right)$ and focus S. Thus harmonic mean will be $\dfrac{2}{\dfrac{1}{AS}+\dfrac{1}{BS}}$ . Thus find AS & BS, simplify it to get the harmonic mean.
Complete step-by-step answer:
We have been given the equation of parabola as \[{{y}^{2}}=8x\]. Now by comparing both general equation and the given equation of the parabola, we cans say that the latus rectum = 4a=8
$\begin{align}
& a=\dfrac{8}{4}=2 \\
& \text{i}\text{.e}\text{. }a=2 \\
\end{align}$
Hence we get a=2.
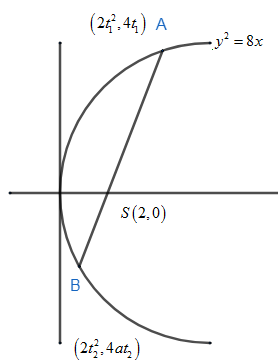
From the figure we can say that $S\left( 2,0 \right)$ is the focus of parabola \[{{y}^{2}}=8x\] .AB is the focal chord of the parabola. Let us take the coordinate of A and B as, put a=2,
$A\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $B\left( at_{2}^{2},2a{{t}_{2}} \right)\Rightarrow $ \[~A\left( 2t_{1}^{2},4{{t}_{1}} \right)\] and $B\left( 2t_{2}^{2},4a{{t}_{2}} \right)$ .
Now, we have been asked to find the harmonic mean of the segment of the focal chord i.e. we need to find the harmonic mean of AS and SB from the figure. The harmonic mean of two numbers x and y are written as, $\dfrac{2}{\dfrac{1}{x}+\dfrac{1}{y}}$ .
Similarly the harmonic mean of AS and BS are written as $\dfrac{2}{\dfrac{1}{AS}+\dfrac{1}{BS}}$ .
Hence from the figure we can say, $AS=2t_{1}^{2}+2$ , $BS=2t_{2}^{2}+2$ .
$\therefore $ Harmonic mean $=\dfrac{2}{\dfrac{1}{AS}+\dfrac{1}{BS}}=\dfrac{2}{\dfrac{1}{2\left( t_{1}^{2}+1 \right)}+\dfrac{1}{2\left( t_{2}^{2}+1 \right)}}=\dfrac{2\times 2}{\dfrac{1}{\left( t_{1}^{2}+1 \right)}+\dfrac{1}{\left( t_{2}^{2}+1 \right)}}$ .
$\therefore $ We got the harmonic means as $\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{1}{t_{2}^{2}+1}}$ .
Here slope of AS= slope of BS
Thus for a focal chord ${{t}_{1}}{{t}_{2}}=-1$ thus, ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$ .
Let us put this in the equation of harmonic means
$\therefore $ Harmonic mean $\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{1}{\dfrac{-1}{{{\left( {{t}_{1}} \right)}^{2}}}+1}}=\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{t_{1}^{2}}{1+t_{1}^{2}}}=\dfrac{4\left( 1+{{t}^{2}} \right)}{\left( 1+{{t}^{2}} \right)}=4$
Thus we got the harmonic mean of the segment of the focal chord as 4.
$\therefore $ Option (D) is the correct answer.
Note: The harmonic mean can be expressed as the reciprocal of the arithmetic mean. Thus, the harmonic mean of segments in the area of parabola means the harmonic mean of AS and BS i.e. of the focal chord AB.
Complete step-by-step answer:
We have been given the equation of parabola as \[{{y}^{2}}=8x\]. Now by comparing both general equation and the given equation of the parabola, we cans say that the latus rectum = 4a=8
$\begin{align}
& a=\dfrac{8}{4}=2 \\
& \text{i}\text{.e}\text{. }a=2 \\
\end{align}$
Hence we get a=2.
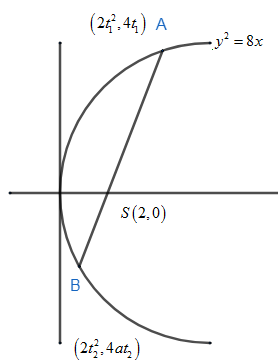
From the figure we can say that $S\left( 2,0 \right)$ is the focus of parabola \[{{y}^{2}}=8x\] .AB is the focal chord of the parabola. Let us take the coordinate of A and B as, put a=2,
$A\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $B\left( at_{2}^{2},2a{{t}_{2}} \right)\Rightarrow $ \[~A\left( 2t_{1}^{2},4{{t}_{1}} \right)\] and $B\left( 2t_{2}^{2},4a{{t}_{2}} \right)$ .
Now, we have been asked to find the harmonic mean of the segment of the focal chord i.e. we need to find the harmonic mean of AS and SB from the figure. The harmonic mean of two numbers x and y are written as, $\dfrac{2}{\dfrac{1}{x}+\dfrac{1}{y}}$ .
Similarly the harmonic mean of AS and BS are written as $\dfrac{2}{\dfrac{1}{AS}+\dfrac{1}{BS}}$ .
Hence from the figure we can say, $AS=2t_{1}^{2}+2$ , $BS=2t_{2}^{2}+2$ .
$\therefore $ Harmonic mean $=\dfrac{2}{\dfrac{1}{AS}+\dfrac{1}{BS}}=\dfrac{2}{\dfrac{1}{2\left( t_{1}^{2}+1 \right)}+\dfrac{1}{2\left( t_{2}^{2}+1 \right)}}=\dfrac{2\times 2}{\dfrac{1}{\left( t_{1}^{2}+1 \right)}+\dfrac{1}{\left( t_{2}^{2}+1 \right)}}$ .
$\therefore $ We got the harmonic means as $\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{1}{t_{2}^{2}+1}}$ .
Here slope of AS= slope of BS
Thus for a focal chord ${{t}_{1}}{{t}_{2}}=-1$ thus, ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$ .
Let us put this in the equation of harmonic means
$\therefore $ Harmonic mean $\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{1}{\dfrac{-1}{{{\left( {{t}_{1}} \right)}^{2}}}+1}}=\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{t_{1}^{2}}{1+t_{1}^{2}}}=\dfrac{4\left( 1+{{t}^{2}} \right)}{\left( 1+{{t}^{2}} \right)}=4$
Thus we got the harmonic mean of the segment of the focal chord as 4.
$\therefore $ Option (D) is the correct answer.
Note: The harmonic mean can be expressed as the reciprocal of the arithmetic mean. Thus, the harmonic mean of segments in the area of parabola means the harmonic mean of AS and BS i.e. of the focal chord AB.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




