Question

The greatest number of points of intersection of 8 lines and 4 circles is:
1) 64
2) 92
3) 104
4) 96

Answer 1

Hint: First of all find out the number of points at which 8 lines can intersect. Next, we find the maximum number of points of intersection of a line and a circle. Then, we find the maximum number of points of intersection of a line and a circle. Add all the points to the greatest number of points of intersection of 8 lines and 4 circles.

Complete step-by-step answer:
As we know that the maximum number of times two lines can intersect is two and similarly a line will intersect a circle at maximum two points.
First, we will find out the number of points at which 8 lines can intersect.
We have selected any 2 lines from the total 8 lines and those lines will make one point of intersection as shown in the figure.

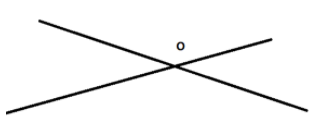
Hence, the number of points of intersection is calculated as,
$^8{C_2} \times 1$
1 is multiplied because the maximum one point of intersection is possible between two lines.
Next, we find the maximum number of points of intersection of a line and a circle.
We can select any one line from 8 lines and anyone circle from 4 circles and they will intersect maximum at two points as given in the figure below.

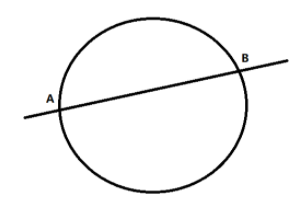
Therefore, the number of points circles and lines can intersect is,
$^8{C_1}{ \times ^4}{C_1} \times 2$
Also, two circles can intersect each other. Two circles can intersect the maximum at two points.

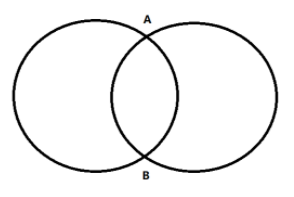
We will select two circles from 4 circles and the maximum number of points of intersection is 2.
Therefore, $^4{C_2} \times 2$
The combination can be calculated using the formula, \[^n{C_r} = \dfrac{{n!}}{{r!\left( {n - r} \right)!}}\]
Add all the points and solve the expression.
$
  ^8{C_2} \times 1{ + ^8}{C_1}{ \times ^4}{C_1} \times 2{ + ^4}{C_2} \times 2 \\
   = \dfrac{{8!}}{{2!6!}} + 2\left( {\dfrac{{8!}}{{1!8!}}} \right)\left( {\dfrac{{4!}}{{1!4!}}} \right) + 2 \times \left( {\dfrac{{4!}}{{2!2!}}} \right) \\
   = 28 + 64 + 12 \\
   = 104 \\
$
Hence, option C is the correct answer.

Note: Since the order of the line or circle does not matter, we will use the combination to calculate the possible number of ways. In this type of questions, students make mistakes by neglecting all possible cases.