Question

The gravitational force between two bodies is $6.67 \times {10^{ - 7}}N$ when the distance between their centres is 10m. if the mass of first body is 800kg, then the mass of second body is:
A. 1000kg.
B. 1250kg.
C. 1500kg.
D. 2000kg.

Answer 1

Hint: To solve this question, we will use Newton's law of gravitation. With a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them, each particle in the universe attracts every other particle. This force works along the two points connecting by the line.

Complete answer:
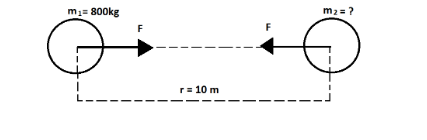
Let us consider two bodies of masses ${m_1}$ and ${m_2}$ and separated by distance r.
According to the law of gravitation, the force of attraction F between them will be,
$F \propto {m_1}{m_2}$ and $F \propto \dfrac{1}{{{r^2}}}$
$ \Rightarrow F \propto \dfrac{{{m_1}{m_2}}}{{{r^2}}}$

We can write this as:
$ \Rightarrow F = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}$ ……… (i)
Where G = universal gravitational constant = $6.67 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$.
Now, given that
Force of attraction, F = $6.67 \times {10^{ - 7}}N$
Distance between two bodies, r = 10m.
Mass of one body, ${m_1}$ = 800kg.
We have to find the mass of the second body (${m_2}$).
Putting these values in equation (i), we will get
\[ \Rightarrow 6.67 \times {10^{ - 7}}N = \dfrac{{6.67 \times {{10}^{ - 11}}N{m^2}k{g^{ - 2}} \times 800kg \times {m_2}}}{{{{10}^2}}}\]
\[ \Rightarrow 6.67 \times {10^{ - 7}}N = \dfrac{{6.67 \times {{10}^{ - 11}}N{m^2}k{g^{ - 2}} \times 800kg \times {m_2}}}{{100}}\]
\[ \Rightarrow 6.67 \times {10^{ - 7}}N \times 100 = 6.67 \times {10^{ - 11}}N{m^2}k{g^{ - 2}} \times 800kg \times {m_2}\]
\[ \Rightarrow \dfrac{{6.67 \times {{10}^{ - 7}}N \times 100}}{{6.67 \times {{10}^{ - 11}}N{m^2}k{g^{ - 2}} \times 800kg}} = {m_2}\]
\[ \Rightarrow {m_2} = 1250kg\]
Hence, we get the mass of the second body, \[{m_2} = 1250kg\]

So, the correct answer is “Option B”.

Note:
Newton's law of gravitation also follows the law of superposition, which states that the gravitational between two masses act independently and uninfluenced by the presence of other bodies. Hence the resultant gravitational force acting on a particle due to a number of masses is the vector sum of the gravitational forces exerted by the individual masses on the given particle. Mathematically, $\overrightarrow {{F_R}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + ...... + \overrightarrow {{F_n}} = \sum\limits_{i = 1}^n {\overrightarrow {{F_i}} } $