Question

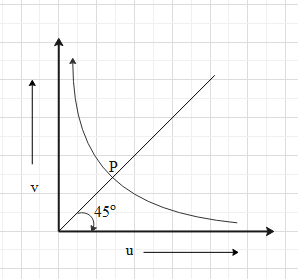
The graph shows variation of v with change in u for a mirror. Points plotted above the point P on the curve are for the values of v

A. smaller than f
B. smaller than 2f
C. larger than 2f
D. larger than f

Answer 1

Hint: Use the mirror formula that gives a relation u, v and f and find an expression for v in the terms of u and f. Then find the relation between v and u at point P. Take a value of v greater than u and find the relation between v and f.
Formula used:
$\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$

Complete answer:
Here, u is the position of the object and v is position of the image with respect to the mirror.
f is the focal length of the mirror.
The relation between u, v and f is given by $\dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{u}$.
$\Rightarrow \dfrac{1}{v}=\dfrac{1}{f}-\dfrac{1}{u}$
$\Rightarrow \dfrac{1}{v}=\dfrac{u-f}{uf}$
$\Rightarrow v=\dfrac{uf}{u-f}$ ….. (i).
From the graph of v v/s u we can understand that as the object comes towards the mirror (as we reduce the object distance), the image distance increases. This means that v is inversely proportional to u.
Let us analyse the relation between u and v at point P. In the graph we can see that the point P also lies on a line passing through the origin and making an angle of ${{45}^{\circ }}$ with the positive x-axis.
From geometry we know that the x and y coordinates of the points on a line passing through the origin and making an angle of ${{45}^{\circ }}$ with the positive x-axis are equal.
This means that at point P, v = u.
Now, since the v is inversely proportional to u and at point P v = u, the value of v will be greater than the value of u for the points above point P.
Therefore, let v = nu, where n is a real number greater than one.
$\Rightarrow u=\dfrac{v}{n}$.
Substitute this value of u in (i).
 $\Rightarrow v=\dfrac{\dfrac{v}{n}f}{\dfrac{v}{n}-f}$
$\Rightarrow \dfrac{v}{n}-f=\dfrac{f}{n}$
$\Rightarrow v-nf=f$
$\Rightarrow v=f+nf$
$\Rightarrow v=(n+1)f$.
But n >1
This means that (n+1) > 2.
This also means that (n+1)f > 2f
This finally means that v > 2f.
Therefore, the value of v is larger than 2f for the points above the point P.

So, the correct answer is “Option C”.

Note:
Other than taking the value of v as v =nu, we can just take some value of v greater than u, say v = 2u.
 $\Rightarrow u=\dfrac{v}{2}$.
Substitute this value of u in (i).
 $\Rightarrow v=\dfrac{\dfrac{v}{2}f}{\dfrac{v}{2}-f}$
$\Rightarrow \dfrac{v}{2}-f=\dfrac{f}{2}$
$\Rightarrow v-2f=f$
$\Rightarrow v=3f$
Substitute u = v in (i).
$\Rightarrow v=\dfrac{vf}{v-f}$
$\Rightarrow v-f=f$
$\Rightarrow v=2f$
This means that the value of v at point P is equal to 2f.
Hence, we can say that the value of v will be greater than 2f above point P.