Question

The graph of \[y = \sin x,\,y = \cos x,\,y = \tan x,\,and\,y = \csc x\] are drawn on the same axes from 0 to $ \dfrac{\pi }{2} $ . A vertical line is drawn through the points where the graphs of $ y = \cos x $ and $ y = \tan x $ cross, intersecting the other graphs at the points A & B. The length of the line segment AB is?

Answer 1

Hint: We are given four trigonometric functions that are drawn on the same axes from 0 to $ \dfrac{\pi }{2} $ . After plotting all the given four functions, we will find the point of intersection of the cosine and tangent functions and then draw a vertical line passing through that point. We will find the length of AB by finding the length of the AC and BC and then subtracting BC from AC.

Complete step by step solution:

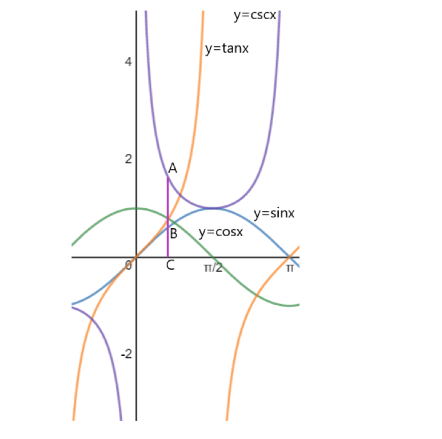
Above is the graph of the four functions on the same axes. B is the point of intersection of $ y = \cos x $ and the vertical line passing through the point of intersection of $ y = \cos x $ and $ y = \tan x $ , and A is the point of intersection of $ y = \csc x $ and the point of intersection of $ y = \cos x $ and $ y = \tan x $ .
At the point of intersection of $ y = \cos x $ and $ y = \tan x $ ,
 $
  \cos x = \tan x \\
   \Rightarrow \cos x = \dfrac{{\sin x}}{{\cos x}} \\
   \Rightarrow {\cos ^2}x = \sin x \\
   \Rightarrow 1 - {\sin ^2}x = \sin x \\
   \Rightarrow {\sin ^2}x + \sin x - 1 = 0 \;
  $
Applying the quadratic formula in the above quadratic equation, we get –
 $
  \sin x = \dfrac{{ - 1 \pm \sqrt {{{(1)}^2} - 4(1)( - 1)} }}{{2(1)}} \\
   \Rightarrow \sin x = \dfrac{{ - 1 \pm \sqrt 5 }}{2} \\
  $
We know that $ - 1 \leqslant \sin x \leqslant 1 $ , so $ \sin x = \dfrac{{ - 1 - \sqrt 5 }}{2} $ is rejected.
So, $ \sin x = \dfrac{{ - 1 + \sqrt 5 }}{2} $
Equation of the line BC is $ y = \sin x $ or $ BC = \dfrac{{ - 1 + \sqrt 5 }}{2} $ and equation of line AC is $ y = \csc x $ or $ AC = \dfrac{1}{{\dfrac{{ - 1 + \sqrt 5 }}{2}}} = \dfrac{2}{{ - 1 + \sqrt 5 }} $
So –
 $
  AB = AC - BC = \dfrac{2}{{ - 1 + \sqrt 5 }} - \dfrac{{ - 1 + \sqrt 5 }}{2} \\
   \Rightarrow AB = \dfrac{{4 - {{(\sqrt 5 - 1)}^2}}}{{2(\sqrt 5 - 1)}} \\
   \Rightarrow AB = \dfrac{{4 - (5 + 1 - 2\sqrt 5 )}}{{2(\sqrt 5 - 1)}} \\
   \Rightarrow AB = \dfrac{{4 - 6 + 2\sqrt 5 }}{{2(\sqrt 5 - 1)}} = \dfrac{{2\sqrt 5 - 2}}{{2\sqrt 5 - 2}} \\
   \Rightarrow AB = 1 \;
  $
Hence the length of AB is 1 unit.
So, the correct answer is “1 unit”.

Note: Trigonometric functions are the functions that tell us the relation between the sides of a right-angled triangle and one of its angles other than the right angle. Sine, cosine, tangent, cosecant, secant and cotangent are the main trigonometric functions. We find the equation of AC and BC as AC passes through cosecant function and BC passes through sine function.