Question

The graph of the function ${({x^2} + {y^2})^2} = 4{x^2}y$ is a double folium as shown below. (a) Find, algebraically, all points on the curve with $y = 1$? (b) Verify that the slopes of tangent lines to both points with $y = 1$ is equal to $0$?

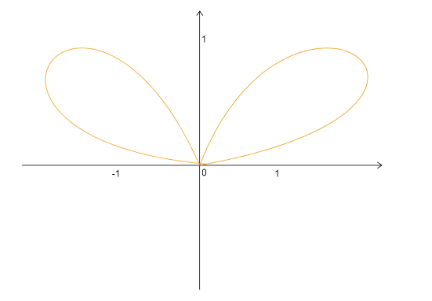
Answer 1

Hint: Start by using the formula $\int\limits_a^b {2\pi rhdx} $ where $a,b$ are the x-bounds. Substitute the values in place of the terms to make the equation easier to solve. Then we will differentiate the term. Now we will substitute these terms in the original expression and integrate.

Complete step by step solution:
We have the given expression of function as ${({x^2} + {y^2})^2} = 4{x^2}y$.
Now we need to evaluate the values of the co-ordinates that is values of $x,y$.
So, we first substitute the value $y = 1$ in the expression ${({x^2} + {y^2})^2} = 4{x^2}y$ and solve for the value of $x$.
$
  {({x^2} + {y^2})^2} = 4{x^2}y \\
   \Rightarrow {({x^2} + {1^2})^2} = 4{x^2}(1) \\
  On\,expanding \\
   \Rightarrow {x^4} + 2{x^2} + 1 = 4{x^2} \\
   \Rightarrow {x^4} - 2{x^2} + 1 = 0 \\
   \Rightarrow {({x^2} - 1)^2} = 0 \\
  Hence, \\
   \Rightarrow {x^2} - 1 = 0 \\
   \Rightarrow {x^2} = 1 \\
   \Rightarrow x = \pm 1 \;
 $
Hence, the coordinates are $(1,1)$ and $( - 1,1)$.

Part b)
Start by using the formula $\int\limits_a^b {2\pi rhdx} $ where $a,b$ are the x-bounds. Substitute the values in place of the terms to make the equation easier to solve. Then we will differentiate the term. Now we will substitute these terms in the original expression and integrate.
If we differentiate implicitly using the chain rule and product rule we will get:
\[2({x^2} + {y^2})\left( {2x + 2y\dfrac{{dy}}{{dx}}} \right) = 4{x^2}\left( {\dfrac{{dy}}{{dx}}} \right) + 8xy\]
But here, we do not need to find an explicit expression for $\dfrac{{dy}}{{dx}}$, just its value when $x = \pm 1$ and $y = 1$. Now we will substitute ${x^2} = 1$ and $y = 1$.
\[
  2(1 + 1)\left( {2x + 2\dfrac{{dy}}{{dx}}} \right) = 4\left( {\dfrac{{dy}}{{dx}}} \right) + 8x \\
  4\left( {2x + 2\dfrac{{dy}}{{dx}}} \right) = 4\left( {\dfrac{{dy}}{{dx}}} \right) + 8x \\
  2x + 2\dfrac{{dy}}{{dx}} = \dfrac{{dy}}{{dx}} + 2x \\
  2\dfrac{{dy}}{{dx}} = \dfrac{{dy}}{{dx}} \\
  \therefore \dfrac{{dy}}{{dx}} = 0 \;
 \]
Hence slopes of tangent lines to both points with $y = 1$ is equal to $0$.

Note: A derivative is the rate of change of a function with respect to a variable. Derivatives are fundamental to the solution of problems in calculus and differential equations. In general, scientists observe changing systems to obtain rate of change of some variable of interest, incorporate this information into some differential equation, and use integration techniques to obtain a function that can be used to predict the behaviour of the original system under diverse conditions. The power rule allows us to find the indefinite integrals of a variety of functions like polynomials, functions involving roots, and even some rational functions.