Question

The graph of quadratic polynomials is ___?

Answer 1

Hint: The graph obtained by plotting a quadratic polynomial comes out to be a Parabola . The roots obtained from solving the quadratic polynomial are the co – ordinates where the parabola cuts the X – Axis . This is because the roots are obtained by putting the given equation equal to zero i.e. where the value of the polynomial is zero .

Complete step-by-step answer:
We know that the standard form of parabola is equals to \[{{f}}\left( {{x}} \right){{ = a}}{{{x}}^{{{2\;}}}}{{ + bx + c}}\] , which also a quadratic polynomial where , \[{{f}}\left( {{x}} \right)\] is a function of \[{{x}}\] . Now , we have to find the roots of the quadratic equation which can find using the formula, \[\left( {\dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}} \right)\] , where \[{{b = }}\]coefficients of \[{{x}}\] , \[{{a = }}\] coefficients of \[{{{x}}^2}\] and \[{{c = }}\]coefficients of \[{{c}}\] in the given quadratic equation . On putting the values we get the roots as , considering the \[a = b = 1,c = - 1\] , we have
\[{{f}}\left( {{x}} \right){{ = }}{{{x}}^{{{2\;}}}}{{ + x - 1}}\] , on applying the above formula , we get
\[{{x = }}\dfrac{{ - 1 \pm \sqrt {{1^2} - 4 \times 1 \times ( - 1)} }}{{2 \times 1}}\]
\[{{x = }}\dfrac{{ - 1 \pm \sqrt {{1^2} + 4} }}{2}\] , on solving we get
\[{{x = }}\dfrac{{ - 1 \pm \sqrt 5 }}{2}\]
This is shows it have real and distinct roots which are
\[{{{x}}_1}{{ = }}\dfrac{{ - 1 + \sqrt 5 }}{2}\]
\[{{{x}}_1}{{ = 0}}.618\] ( approx. )
  and \[{{{x}}_2}{{ = }}\dfrac{{ - 1 - \sqrt 5 }}{2}\]
\[{{{x}}_2}{{ = }} - 1.618\] (approx.)
Now , on plotting the graph of \[{{f}}\left( {{x}} \right){{ = }}{{{x}}^{{{2\;}}}}{{ + x - 1}}\] , we get

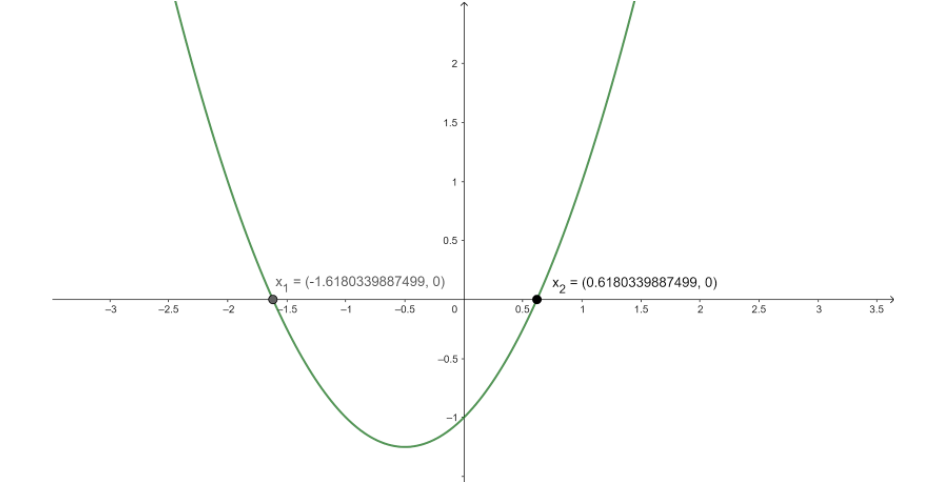
The intercepts at X – axis are roots of the equation . Also the graph of the equation symbolizes the shape of a parabola .

Note: The graph of a quadratic polynomial depends upon the degree of the polynomial such as if we have two variables with degree as \[2\] then the shape of the graph will be ellipse , also the roots of a quadratic equation can be of different types which depends on discriminant of Quadratic formula which is \[\sqrt {{b^2} - 4ac} \] , it is equals to zero we have real and equal roots . If it is greater than zero we have real and unequal roots . If the discriminant is less than zero we have complex roots .