Question

The graph of line $y = 6$ is a line that is:
A.Parallel to the $x$axis at a distance of 6 units from the origin.
B.Parallel to $y$axis at a distance of 6 units from the origin
C.Making an intercept of 6 units on the $x$axis
D.Making an intercept of 6 units on the both the axes

Answer 1

Hint: Hint: The equation $y = 6$ can be written as $y = 0x + 6$. Find the value of $y$ for different values of $x$ such as \[ - 1,0,1,2..\]. Then draw the line in the $xy$ plane.

Complete step-by-step answer:
The equation given to us in the question $y = 6$ can be rewritten as $y = 0x + 6$.
We can then find different ordered pair that satisfies the equation $y = 0x + 6$ by finding the different values of $y$ for different integer values of $x$ such as \[ - 1,0,1,2..\]
For\[x = 0\], $y = 6$
\[x = 1\], $y = 6$
\[x = 2\], $y = 6$
\[x = 3\], $y = 6$

The different ordered pairs so formed are$\left( {0,6} \right),\left( {1,6} \right),\left( {2,6} \right),\left( {3,6} \right)$.

We can draw the line in the $xy$ plane by plotting different points and joining them to form the line.

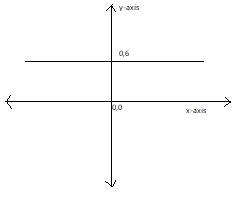
From the diagram we can observe that the line never touches the $x$ axis.
Therefore there is no intercept on the $x$ axis. Since there is no intercept on the $x$ axis the given line is parallel to the $x$ axis.
Also, we can observe that the distance between the $x$ axis and the given line is 6 units throughout.

Therefore we can conclude the given line is parallel to $x$ axis at a distance of 6 units from the origin.
Thus, option A is the correct answer.

Note: The graph of any equation of one variable can be plotted on the $xy$ plane. The $x$ axis is the horizontal axis and $y$ axis is the vertical axis. The intersection of $x$ and $y$ axis is called the origin