Question

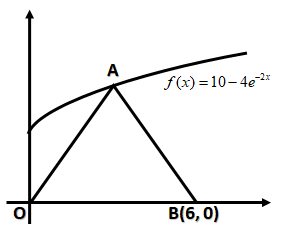
The graph of \[f(x) = 10 - 4{e^{ - 2x}}\] is shown. What is the area of triangle ABO if OA=OB.

A.25
B.60
C.45
D.50
E.30

Answer 1

Hint: To find the area of a triangle we will apply the formula of the area of the triangle. For that we have to draw a line perpendicular on OB at point C and passes from A. First of all, find the coordinates of A from the given condition i.e. \[OA = AB\]. After we know the coordinates of A and C, we can calculate the value of AC. Then finally we can calculate area of $\vartriangle ABO$ and formula for area of triangle is given by:
$ \Rightarrow A = \dfrac{1}{2} \times b \times h$

Complete step-by-step answer:
In this question we have given with the graph of \[f(x) = 10 - 4{e^{ - 2x}}\]as shown below:

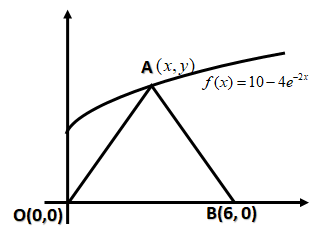
Let us assume the coordinates of A be $(x,y)$. We can find it by the following steps:
As, O is at origin. Therefore, the coordinate of O is $(0,0)$. B point lies on $(6,0)$.
The distance between two coordinates $O(0,0)$ and $A(x,y)$ i.e. OA can be calculated as:
$ \Rightarrow OA = \sqrt {{{(x - 0)}^2} + {{(y - 0)}^2}} $
While opening the bracket, we get,
$ \Rightarrow OA = \sqrt {{x^2} + {y^2}} $ ……(1)
And the distance between two coordinates $A(x,y)$and $B(6,0)$ i.e. AB can be calculated as:
$ \Rightarrow AB = \sqrt {{{(x - 6)}^2} + {{(y - 0)}^2}} $
While opening the bracket, we get,
$ \Rightarrow AB = \sqrt {{x^2} + 36 - 12x + {y^2}} $ ……(2)
As it is given that \[OA = AB\], therefore by putting the values of (1) and (2) in this we get,
\[ \Rightarrow OA = AB\]
$ \Rightarrow \sqrt {{x^2} + {y^2}} = \sqrt {{x^2} + 36 - 12x + {y^2}} $
By squaring both sides we get,
$ \Rightarrow {x^2} + {y^2} = {x^2} + 36 - 12x + {y^2}$
By cancelling same terms from both sides, we get,
$ \Rightarrow 0 = 36 - 12x$
Taking term of x on L.H.S we get,
$
   \Rightarrow 12x = 36 \\
   \Rightarrow x = 3 \\
$

To find y, put $x = 3$ in \[f(x) = 10 - 4{e^{ - 2x}}\] we get,
$ \Rightarrow y = 10 - 4{e^{ - 2(3)}}$
$ \Rightarrow y = 10 - 4{e^{ - 6}}$ ……..(3)
To find area of $\vartriangle ABO$, we have to find base i.e. OB and height. For height we will draw a line perpendicular on OB at point C and passes from A as shown below:

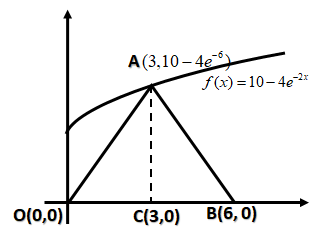
We can find the OB i.e.
$
   \Rightarrow OB = \sqrt {{{(6 - 0)}^2} + {{(0 - 0)}^2}} \\
   \Rightarrow OB = \sqrt {{6^2}} \\
$
By cancelling square root with square of 6 we get,
$ \Rightarrow OB = $6 ……(4)
We can calculate the AC as:
$ \Rightarrow AC = \sqrt {{{(3 - 3)}^2} + {{(10 - 4{e^{ - 6}} - 0)}^2}} $
By solving and opening the bracket, we get,
$ \Rightarrow AC = \sqrt {{{(10 - 4{e^{ - 6}})}^2}} $
By cancelling square root with square, we get,
$ \Rightarrow AC = 10 - 4{e^{ - 6}}$ ……(5)
The area of $\vartriangle ABO$ is given by
$ \Rightarrow A = \dfrac{1}{2} \times OB \times AC$
By putting the values of (4) and (5) in above equation we get,
$ \Rightarrow A = \dfrac{1}{2} \times 6 \times (10 - 4{e^{ - 6}})$
By dividing 6 with 2 we get,
$ \Rightarrow A = 3(10 - 4{e^{ - 6}})$
Put value of ${e^{ - 6}} = 0.00247$ in above equation we get,
$ \Rightarrow A = 3(10 - 4 \times 0.00247)$
$ \Rightarrow A = 3(10 - 0.00991)$
We will take approximation in this by ignoring decimal value as it is very small, hence
$ \Rightarrow A \approx 3 \times 10$
$ \Rightarrow A \approx 30$
Hence, option E is the correct answer.

Note: Here students get confused while finding the coordinates of A. They do mistake at this point as they take y coordinate as zero because while finding the A coordinates the answer will be left only with x value. But as A lies on the graph of \[f(x) = 10 - 4{e^{ - 2x}}\]. Hence y is defined as a function of x and we can find the y coordinate for A by putting the value of x i.e. 3 in the function \[f(x)\] and hence the value of y is \[10 - 4{e^{ - 6}}\].