Question

The graph of a linear equation in x and y passes through A (-1, -1) and B (2, 5). From your graph, find the values of h and k if the line passes through (h, 4) and $ \left( {\dfrac{1}{2},k} \right) $ .

Answer 1

Hint: Given the graph of the linear equation in x and y passes through two points. The line equation when two points are given is $ y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right) $ where (x1, y1) is the first point and (x2, y2) is the second point. Use this line equation form to find the line equation. Substitute the known values in this equation to find the value of unknown values.

Complete step-by-step answer:

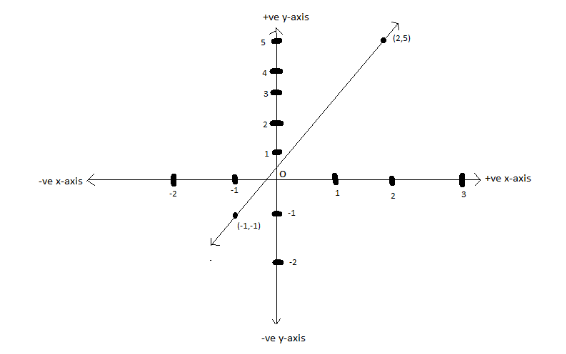
We are given that the graph of a linear equation in x and y passes through A (-1, -1) and B (2, 5).
We have to find the line equation using $ y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right) $
The line equation is
 $
  y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right) \\
  y - \left( { - 1} \right) = \dfrac{{5 - \left( { - 1} \right)}}{{2 - \left( { - 1} \right)}}\left( {x - \left( { - 1} \right)} \right) \\
  y + 1 = \dfrac{{5 + 1}}{{2 + 1}}\left( {x + 1} \right) \\
  y + 1 = 2\left( {x + 1} \right) \\
  y + 1 = 2x + 2 \\
  y = 2x + 1 \\
  $
Therefore, the line equation is $ y = 2x + 1 $
We have to find the value of h in (h, 4). The line also passes through (h, 4)
 $
  y = 2x + 1 \\
  4 = 2h + 1 \\
  2h = 3 \\
  h = \dfrac{3}{2} \\
  $
We have to find the value of k in $ \left( {\dfrac{1}{2},k} \right) $ . The line passes through $ \left( {\dfrac{1}{2},k} \right) $
 $
  y = 2x + 1 \\
  k = 2\left( {\dfrac{1}{2}} \right) + 1 \\
  k = 1 + 1 \\
  k = 2 \\
  $
The value of h is 3/2 and the value of k is 2.

Note: Linear equations in two variables will have maximum two variables. There are many ways to find the equation of a line in two variables. We used two points form in the above solution. Other forms are slope-intercept form, intercept form, slope-point form and standard form.