Question

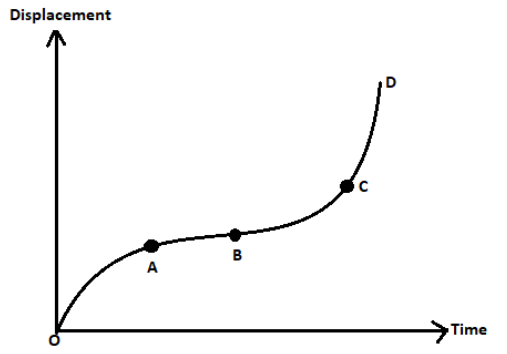
The graph between the displacement x and time t for a particle moving in a straight line as shown in the figure. During the interval, OA, AB, BC, and CD, the acceleration of the particle is:

(A). +0++
(B). -0+0
(C). +0-+
(D). -0-0

Answer 1

Hint: In this question, we need to start with finding the slope of the graph for a different branch. And the nature of slope gives us the knowledge of velocity, that is if slope is increasing, decreasing, or constant accordingly velocity will be increasing, decreasing, or constant respectively. Now using this we can find the acceleration that is velocity is increasing acceleration is +, if decreasing acceleration is -, and if remaining constant acceleration is 0.

Complete step-by-step solution -
Let displacement be \[x\] and time be $t$ now we know that differentiation of displacement with respect to time gives us the velocity $v$ of the body.
$v = \dfrac{{dx}}{{dt}}$
And it can be seen from the graph that the slope of the displacement vs time graph is velocity.
$slope = \dfrac{{dx}}{{dt}} = v$
Now we will see one by one the nature of the slope of each part in the graph
From the graph, we can see that the slope of the branch OA is decreasing which implies velocity is decreasing, and therefore acceleration is negative (-).
When the slope is constant as can be seen in the branch AB implies that the velocity is not changing. Therefore the acceleration is zero (0).
Similarly, the slope of branch BC is increasing it means velocity is increasing, and therefore acceleration is positive (+).
At last, we can see that the slope of branch CD is constant so here also the velocity remains constant and therefore acceleration is zero (0).
Therefore the correct answer is option is B that is -0+0.

Note: For these types of questions initially we need to know the basics of the graphs that are the slope of displacement vs time gives velocity, area of acceleration time graph also gives velocity, area of velocity vs time graph gives displacement, etc. Then we need to know how the variation in velocity affects the acceleration.