Question

The graph between \[\sqrt {{E_k}} \] and $\dfrac{1}{p}$ is
(${E_x} = $ Kinetic energy and $P = $Momentum)
A.

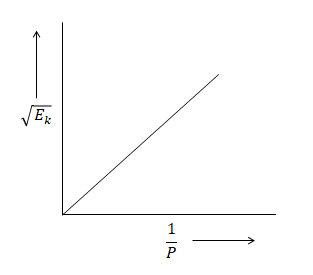
B.

C.

D.

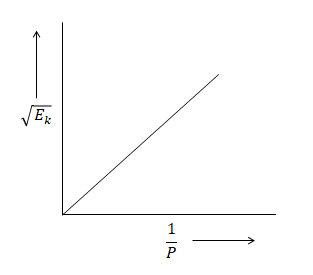
Answer 1

Hint: Kinetic energy is directly proportional to the mass of the thing and to the face of its velocity. If the mass has units of kilograms and therefore, the velocity of meter per second, the K.E. has a unit of kilogram meter squared per second squared.
When the given graph is drawn between the root of kinetic energy and one divided by momentum.

Complete step-by-step solution:
Kinetic energy is that the energy that any substance has when it accelerates, whereas momentum is an object's mass in motion. There is a Kinetic energy and momentum relation thanks to their reference to mass and velocity.
$ \Rightarrow {E_K} = \dfrac{1}{2}m{v^2}$
Taking cross multiplication we get,
$ \Rightarrow 2{E_K} = m{v^2}$
On multiply \[m\]on both sides we get,
$ \Rightarrow 2m{E_K} = {m^2}{v^2}$
Here,\[mv = p\]
Putting the value, we get
$ \Rightarrow 2m{E_K} = {p^2}$
Now take a root from both sides,
$ \Rightarrow \sqrt {2m{E_K}} = P$
on dividing we get
$ \Rightarrow \sqrt {{E_K}} = \dfrac{P}{{\sqrt {2m} }}$
Taking cross multiplication we get,
$ \Rightarrow \dfrac{{\sqrt {{E_k}} }}{p} = \dfrac{1}{{\sqrt {2m} }} = $Constant
$ \Rightarrow \left( {\sqrt {{E_K}} } \right) \times \left( {\dfrac{1}{P}} \right) = $Constant
If \[XY{\text{ }} = \] constant is a hyperbolic graph with only the upper side in the positive X- axis because $\sqrt {{E_K}} $ is always positive value.

So, the graph option A is correct.

Additional Information: The relationship between kinetic energy and momentum
It depends on two variables – velocity and mass of an object. There is a relation between Kinetic energy and momentum as both the properties are linked with velocity. Momentum gets expressed as a multiplication of velocity and mass, whereas K.E is the product of the square of speed and half the mass.

Note: If a huge particle and a light-weight particle have an equivalent momentum, the sunshine one will have tons more Kinetic energy. If a light-weight particle and an important one have an equivalent velocity, the heavy one has more Kinetic energy.