
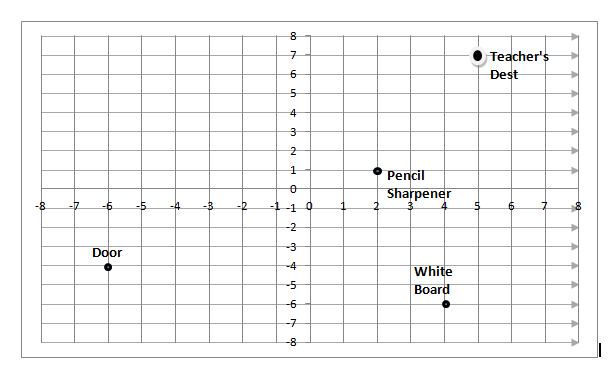
The graph below shows the place in the math classroom. Each unit presents $1$ foot. What is the distance, in feet, between the pencil sharpener and the door? Round your answer nearest to the tenth.

Answer
543.6k+ views
Hint: Here, we can get the distance between the pencil sharpener and the door by using the formula $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ , where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the coordination of the first object and $\left( {{x}_{2}},{{y}_{2}} \right)$ is the coordination of the second object. So, we will find out the coordinates of the pencil sharpener and the door respectively. Then we will get the distance by using the formula.
Complete step by step solution:
Since, we need to find the distance between the pencil sharpener and the door. So, we will use the formula for that we need the coordination of the pencil sharpener and the door.
Here, we already have the graph in which we can see the coordination of the pencil sharpener and the door as:
Coordination of the pencil sharpener $=\left( 2,1 \right)$
Because the point lies where it covers $2$ unit from y axis in the direction of x axis and covers $1$ unit from x axis in the direction of y axis.
Similarly, the coordination of the door $=\left( -6,-3 \right)$
Because the point lies where it covers $6$ unit from y axis in the negative direction of x axis and covers $3$ unit from x axis in the negative direction of y axis.
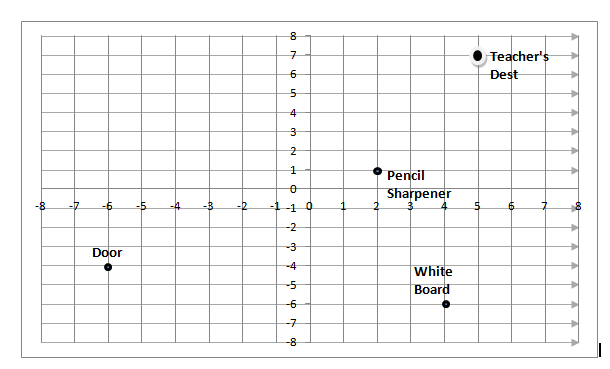
Here we got the coordination. So we will use the formula that is:
$=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Here, we will consider the coordination of pencil sharpener $\left( {{x}_{1}},{{y}_{1}} \right)$ and coordination of door $\left( {{x}_{2}},{{y}_{2}} \right)$ and will use them in the above formula as:
$=\sqrt{{{\left( -6-2 \right)}^{2}}+{{\left( -3-1 \right)}^{2}}}$
Now, we will do addition for bracketed terms because they have same sign as:
$=\sqrt{{{\left( -8 \right)}^{2}}+{{\left( -4 \right)}^{2}}}$
Here, we will square them and will get positive value as:
$=\sqrt{64+16}$
Now, the sum of $64$ and $16$ is $80$ as:
$=\sqrt{80}$
Since, $80$ is not a perfect square no. So we will get the square root of $80$ as:
$=4\sqrt{5}$
Here, we can replace $\sqrt{5}$ by putting its value that is $2.236$ as:
$=4\times 2.236$
After doing multiplication we will have:
$=8.944$
Since, each unit presents $1$ foot. So, we don’t need any other calculation.
Hence, the distance, in feet, between the pencil sharpener and the door is $8.94$ feet.
Note: For this type of question where we need to find the distance between two points, we will use the formula of distance between two points that is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ and where we can choose any one coordination of any point as $\left( {{x}_{1}},{{y}_{1}} \right)$ . So, we will choose any coordination as $\left( {{x}_{1}},{{y}_{1}} \right)$, normally other will be $\left( {{x}_{2}},{{y}_{2}} \right)$ itself.
Complete step by step solution:
Since, we need to find the distance between the pencil sharpener and the door. So, we will use the formula for that we need the coordination of the pencil sharpener and the door.
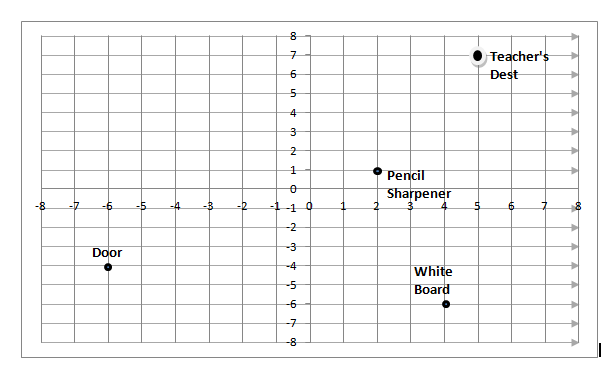
Here, we already have the graph in which we can see the coordination of the pencil sharpener and the door as:
Coordination of the pencil sharpener $=\left( 2,1 \right)$
Because the point lies where it covers $2$ unit from y axis in the direction of x axis and covers $1$ unit from x axis in the direction of y axis.

Similarly, the coordination of the door $=\left( -6,-3 \right)$
Because the point lies where it covers $6$ unit from y axis in the negative direction of x axis and covers $3$ unit from x axis in the negative direction of y axis.

Here we got the coordination. So we will use the formula that is:
$=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Here, we will consider the coordination of pencil sharpener $\left( {{x}_{1}},{{y}_{1}} \right)$ and coordination of door $\left( {{x}_{2}},{{y}_{2}} \right)$ and will use them in the above formula as:
$=\sqrt{{{\left( -6-2 \right)}^{2}}+{{\left( -3-1 \right)}^{2}}}$
Now, we will do addition for bracketed terms because they have same sign as:
$=\sqrt{{{\left( -8 \right)}^{2}}+{{\left( -4 \right)}^{2}}}$
Here, we will square them and will get positive value as:
$=\sqrt{64+16}$
Now, the sum of $64$ and $16$ is $80$ as:
$=\sqrt{80}$
Since, $80$ is not a perfect square no. So we will get the square root of $80$ as:
$=4\sqrt{5}$
Here, we can replace $\sqrt{5}$ by putting its value that is $2.236$ as:
$=4\times 2.236$
After doing multiplication we will have:
$=8.944$
Since, each unit presents $1$ foot. So, we don’t need any other calculation.
Hence, the distance, in feet, between the pencil sharpener and the door is $8.94$ feet.
Note: For this type of question where we need to find the distance between two points, we will use the formula of distance between two points that is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ and where we can choose any one coordination of any point as $\left( {{x}_{1}},{{y}_{1}} \right)$ . So, we will choose any coordination as $\left( {{x}_{1}},{{y}_{1}} \right)$, normally other will be $\left( {{x}_{2}},{{y}_{2}} \right)$ itself.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

10 examples of friction in our daily life




