Question

The graph below shows the height of a tunnel $ f(x) $ in feet, depending on the distance from one side of the tunnel $ x $ , in feet?

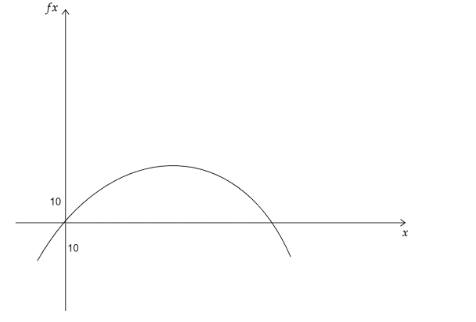
Part A: What do the x-intercepts and maximum value of the graph represent? What are the intervals where the function is increasing and decreasing, and what do they represent about the distance and height?

Part B: What is an appropriate average rate of change of the graph from $ x = 20 $ to $ x = 35 $ , and what does this rate represent?

A.

Answer 1

Hint: Start by explaining all the basic terms of the terms like x-intercept, y-intercept. Then evaluate the highest, middle and the lowest point. Evaluate when the function is increasing and decreasing in the graph. Form inequalities and then evaluate.

Complete step by step solution:
Here, the x-intercepts, where the value is $ 0 $ , represents where the sides of the tunnel meet the floor of it.
Also, the maximum $ y $ value represents the middle of the tunnel and its highest point that is something between $ 35 $ and $ 40 $ feet. The interval where the given function is increasing is given by $ 0 \leqslant x \leqslant 60 $ and the interval where its decreasing is $ 60 \leqslant x \leqslant 120 $ . Now, where the function increases, the height of the tunnel is increasing that is towards the middle of the tunnel and where its decreasing and the height is decreasing that is towards the right edge of the tunnel.

Note: While splitting the term be careful. While evaluating the intervals make sure to get the exact point. Pay attention to the types of brackets you are using. Remember the types of brackets are open and closed which are denoted by $ (\,) $ and $ \,[\,] $ .

B.
Hint: Start by explaining all the basic terms of the terms like x-intercept, y-intercept. Then evaluate the highest, middle and the lowest point. Evaluate when the function is increasing and decreasing in the graph. Form inequalities and then evaluate.

Complete step by step solution:
When $x = 20,\,y = 20$ and $x = 35,\,\,y = 30$.
The approximate rate of change then is given by,
 $ \dfrac{{change\,\,in\,\,y}}{{change\,\,in\,\,x}} $ or we can write it as,
   $
   = \dfrac{{30 - 20}}{{35 - 20}} \\
   = \dfrac{{10}}{{15}} \\
   = \dfrac{2}{3} \\
   = .\overline 6 \;
  $
Now, this means that from $ 20 $ feet from the left of the tunnel to roughly $ 35 $ from the left of the tunnel, that for every $ 3 $ feet you move across the floor of the tunnel, the height of the tunnel rises up to $ 2 $ feet or we can also say that it is the slope of the roof of the tunnel at that point in the tunnel.

Note: While substituting the terms make sure you are taking into account the degrees and signs of the terms as well. While applying the power rule make sure you have considered the power with their respective signs.