Question

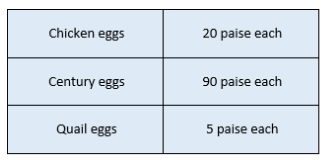
The given table shows the prices of 3 different types of eggs. Priya bought some eggs, out of which $\dfrac{1}{4}$ were chicken eggs, $\dfrac{1}{8}$ were century eggs and rest were Quail eggs. If Priyanka spent a total amount of Rs. 6.50 on the chicken and century eggs, how much did he spend in total.

Answer 1

Hint: Start by letting the total number of eggs bought by Priya to be x eggs. So, using the data given in the question, we can say that the number of chicken eggs is equal to $\dfrac{1}{4}x$ and the number of century eggs is equal to $\dfrac{1}{8}x$ . Also, use the condition given in the question that she spent Rs. 6.50 on century and chicken eggs to get the value of x. Once you get x, subtract the number of century and chicken eggs from it to get the number of quail eggs which when multiplied by the price of each quail egg given the amount spent on quail eggs. Add the amount with Rs. 6.50 to get the answer.

Complete step-by-step solution -
Let us start to the solution to the above question by letting the total number of eggs bought by Priya to be x eggs.
Now as it is given that Priya bought some eggs, out of which $\dfrac{1}{4}$ were chicken eggs, $\dfrac{1}{8}$ were century eggs so, we can say that the number of chicken eggs is equal to $\dfrac{1}{4}x$ and the number of century eggs be $\dfrac{1}{8}x$ .
It is also given that a total amount of Rs. 6.50, i.e., 650 paise was spent on the chicken and century eggs. Looking at the table we also know that the cost of one chicken egg is 20 paise and one century egg is 90 paise. So, the equation we get is
$\dfrac{1}{4}x\times 20+\dfrac{1}{8}x\times 90=650$
$\Rightarrow \dfrac{2}{8}x\times 2+\dfrac{1}{8}x\times 9=65$
$\Rightarrow \dfrac{13}{8}x=65$
$\Rightarrow x=65\times \dfrac{8}{13}$
$\Rightarrow x=40eggs$
So, we can say that altogether Priya had bought 40 eggs.
Therefore, the number of chicken eggs is $\dfrac{1}{4}x=\dfrac{1}{4}\times 40=10$ and the number of century eggs is $\dfrac{1}{8}x=\dfrac{1}{8}\times 40=5$ . So, the number of quail eggs is 40-10-5=25. Also, from the table the cost of each quail egg is 5 paise. So, the cost of 25 quail eggs is $5\times 25=125paise=Rs.\text{ }1.25$
So, the total amount spent is:
cost of quail eggs + cost of century eggs + cost of chicken eggs.
The combined cost of chicken and century egg is Rs. 6.50 and that of the quail egg is Rs. 1.25.
$Total\text{ }\cos t=6.50+1.25=\text{Rs}\text{. }7.25$
Therefore, the answer to the above question is Rs. 7.25.

Note: The key to the above question was to select the element of the question that you will treat as variable. We selected the total number of eggs to be the variable as we had the fractions of the different eggs given, so as we considered the total number as the variable, we indirectly knew the numbers of eggs in terms of the taken variables. Remember that you need to convert all the elements given in the question to a single unit system, as we converted all the costs to pay for avoiding errors. We used 100 paise = Rs. 1 for the required conversion.