Question

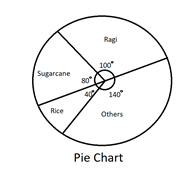
The given pie chart shows annual agricultural yield of certain places. If the total production is $8100$ ${\text{tons}}$, then what is the yield of Ragi in ${\text{tons}}$?

A) $225$ ${\text{tons}}$
B) $2250$ ${\text{tons}}$
C) $22.5$ ${\text{tons}}$
D) $2.250$ ${\text{tons}}$

Answer 1

Hint: In this question, we are given a pie chart which is divided into four sections. Each section has a name with degrees written in it. We are also told the total production and we have been asked the yield of ragi. Use the degrees to find the answer. Since the degrees of ragi is $100^\circ $ and total is $360^\circ $, divide 110 by 360 and multiply it by the total production to find the answer.
Or you can use the $2^{nd}$ method. In this method, we use a unitary method to find the value of $1^\circ $ as we know that $360^\circ = 8100 {\text{tons}}$. Then, we multiply the value of $1^\circ $ by 100 to find the value of $100^\circ $.

Complete step-by-step solution:
We are given a pie chart with four sections. Each section represents an agricultural yield of some place. We have been asked for the yield of ragi. Ragi represents $100^\circ $ out of $360^\circ $. The total yield can be founded by dividing $100^\circ $ by $360^\circ $ and multiplying it by $8100 {\text{tons}}$
$ \Rightarrow \dfrac{{100^\circ }}{{360^\circ }} \times 8100$
Simplifying,
$ \Rightarrow 2250 {\text{tons}}$

Therefore, the total yield of ragi is $2250 {\text{tons}}$.

Note: This question can also be solved by unitary method. Under this method, we know that the entire pie chart represents 8100 tons and it also represents $360^\circ $. Using this fact, we will get the value of $1^\circ $, and then we will multiply it with $100^\circ $.
We know that-
$ \Rightarrow 360^\circ = 8100{\text{tons}}$
Finding the value of $1^\circ $using unitary method,
$ \Rightarrow 1^\circ = \dfrac{{8100}}{{360}}$
$ \Rightarrow 1^\circ = 22.5{\text{tons}}$
Multiply both the sides by 100 to find the value of $100^\circ $,
$ \Rightarrow 100^\circ = 22.5 \times 100{\text{tons}}$
$ \Rightarrow 100^\circ = 2250{\text{tons}}$
Therefore, the total yield of ragi is $2250{\text{tons}}$.