Question

The given hinge construction consists of two rhombus with the ratio of sides $3:2$. The vertex $C$ moves in the horizontal direction with a velocity $v$. The velocity of $B$ is then

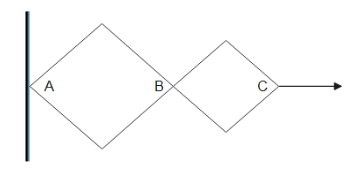
A. $0.3v$
B. $0.6v$
C. $2v$
D. $3v$

Answer 1

Hint: We are given a hinge construction consisting of two rhombi of sides of a certain ratio and the vertex of the later rhombus moves with the given velocity and we need to find the velocity of the second vertex. We need to use the properties of two rhombi and compare the ratio of the corresponding sides with the velocities of the vertices.

Complete step by step answer:
 We will redraw the given diagram to get a clear understanding of the given situation.

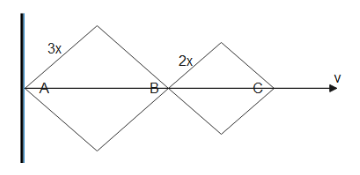
We joined the segments AB and BC and since the ratio of the sides of the two rhombi is $3:2$ hence by the geometry of two rhombi we get
$\dfrac{{3x}}{{2x}} = \dfrac{{AB}}{{BC}} = \dfrac{3}{2}$
Hinge $B$ pulls the segment AB and the hinge $C$ pulls the segment AC.Hence
$\dfrac{{AB}}{{BC + AB}} = \dfrac{3}{{2 + 3}} = \dfrac{3}{5}$
Now it is given that the vertex C moves with velocity $v$ , the vertex B will also move with similar velocity along the segment, therefore
$\dfrac{{{V_B}}}{{{V_C}}} = \dfrac{3}{5}$
$ \Rightarrow {V_B} = \dfrac{3}{5}{V_C} \\
\Rightarrow {V_B}= \dfrac{3}{5}V \\
\therefore {V_B}= 0.6v$

Hence option B is the correct answer.

Note: Note that in a rhombus, all the sides are equal. Like squares, rhombuses satisfy the condition of the ratio of corresponding sides being equal. In a rhombus, the opposite sides are parallel and hence the opposite angles are equal. But the value of the angles can be anything except right angles otherwise it will be a square. Therefore all rhombuses are not similar and we cannot compare the corresponding sides of two random rhombi. We use the geometry of two rhombi because the ratio of the sides was given in the question.