Question

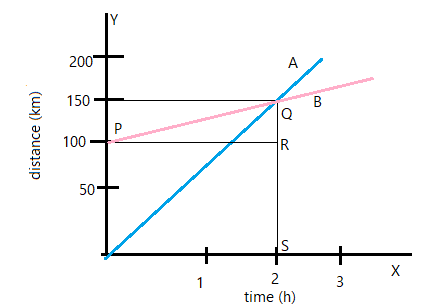
The given figure shows the distance-time graphs of two trains, which start moving simultaneously in the same direction, from the graphs, find:
i. How much B is ahead of A when motion starts?
ii. What is the speed of B?
iii. When and where A will catch B?
iv. What is the difference in speed of A and B?

Answer 1

Hint: We know that speed is defined as the rate at which distance varies with respect to time. Clearly, function of distance and time. Or speed depends directly on the parameters distance and time. Using this idea, we can solve this sum.

Formula used: speed=$\dfrac{\text{distance}}{\text{time}}$

Complete step by step answer:
Clearly, from the definition, speed depends on the ratio of the two. Here we have a graph between the distance and time of two moving objects A and B. Then the slope of this given graph gives the speed of moving objects A and B.

i) From the graph, when $t=0$ , $A$ is at $100\;km$ and $B$ is at $0\;km$. Then we can say that $A$ is ahead of $B$ by $100\;km$ .
ii) From the graph, we can say that $B$ covers $150\;km$ in $2\;hr$ then the speed of $B$ is given as $v_{B}=\dfrac{150}{2}=75km/hr$
iii) Since at $Q$ the graph of $A$ and $B$ intersects, we can then say that, at $t=2hr$ and at $d=150km$ $A$ and $B$ meet.
iv) From ii) $v_{B}=75km/hr$
Similarly, from triangle $P\;Q\;R$ we can say that $v_{A}=\dfrac{150-100}{2}=\dfrac{50}{2}=25km/hr$

Then the difference between, $v_{B}-v_{A}=75-25=50km/h$

Note: This is a very easy sum. One needs to understand the graph to solve this sum. Also note that the $speed=\dfrac{distance}{time}$, since the given graph is distance-time graph, we can say that the solve of the graph gives the speed of the objects. This is used to solve the questions ii) and iv). Also, note that the steeper the graph, implies more the speed of the body. Here, clearly object B has more speed or is faster than that of A. Since A started at $100\;km$, it is quite clear that the speed of B must be greater than that of A, only then B can catch up with A.