Question

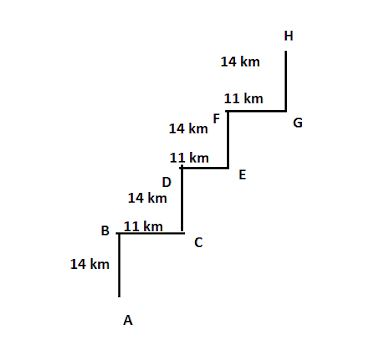
The given figure shows the distances covered by Ariv from place A to place H. His direction of movement from A to B, C to D, F to F and G to H is due North and that B to C, D to E and F to G is due East.Find the aerial distance between A and H.

(a) 34 km
(b) 65 km
(c) 55 km
(d) None of these

Answer 1

Hint: To start with, we are here with a figure, where we are to find a distance between the first point and the last point. The distances between some specific points are given and we are to find the total distance. So, to solve this problem we will try to join the first and the last point so that we find the shortest distance between those points. We also try to make it a right angled triangle so that we can use the Pythagoras theorem to find the distance.

Complete step by step solution:
According to the problem, here we are given a figure where the distances between some specific points are given. We can see, GH = EF = CD = AB = 14 km and BC = DE = FG = 11 km.
We are to find the distance between A and H.
So, let us join A and H.
Again, let us also consider a point O such that $\angle AOH=90{}^\circ $ .
Thus, we are getting a triangle AOH where$\angle AOH=90{}^\circ $, so this is a right angled triangle.
And now, we will try to find the length of the hypotenuse.
As per the Pythagoras’s theorem, ${{c}^{2}}={{a}^{2}}+{{b}^{2}}$ , where c is the hypotenuse and a and b are the other two sides of the triangle.
So, to find AH we have to first find AO and OH.
Then, AO = BC + DE + FG
So, we have, AO = $\left( 11\times 3 \right)km=33km$
Again, OH = AB + CD + EF + GH
Thus, we get, OH = $\left( 14\times 4 \right)km=56km$
So, now we are getting, ${{\left( AH \right)}^{2}}={{\left( AO \right)}^{2}}+{{\left( OH \right)}^{2}}$
Putting the values, ${{\left( AH \right)}^{2}}={{\left( 33 \right)}^{2}}+{{\left( 56 \right)}^{2}}$
Simplifying we get, ${{\left( AH \right)}^{2}}=1089+3136=4225$
Thus getting, AH = $\sqrt{4225}=65km$

So, the correct answer is “Option (b)”.

Note: Here we are using the Pythagoras theorem to get the solution of your problem. Pythagora's theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides''. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle of 90 degree. The sides of a right triangle (say, a, b and c) which have positive integer values, when squared, are put into an equation, also called a Pythagorean triple.