Question

The given figure shows a small garden. The shaded area is reserved for planting flowers and the rest of the area is for grass, find the ratio of the area of the garden reserved for planting flowers to the area reserved for grass.

Answer 1

Hint: First we’ll find the total area and the area reserved for flowers, then their difference will be the area reserved for grass.
After finding the area reserved for grass and flowers, we’ll find it’s ratio to get the required answer.

Complete step-by-step answer:

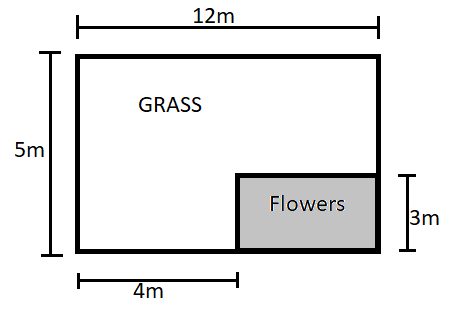
Dimension of area for flowers is (12-4)m by 3m i.e. 8m by 3m
The dimension of total area is 12m by 5m
We know that,
\[Area{\text{ }}of{\text{ }}rectangle = \left( {length} \right)\left( {breadth} \right)\]
Therefore, the area of the garden reserved for flowers= $8m \times 3m$
$ = 24{m^2}$
\[Total{\text{ }}area = \]$12m \times 5m$
$ = 60{m^2}$
From the given figure we can say that the area reserved for grass is equal to the difference of the total area and the area that is reserved for flowers
\[Area{\text{ }}reserved{\text{ }}for{\text{ }}grass = \]$60{m^2} - 24{m^2}$
$ = 36{m^2}$
Therefore the ratio of the area of the garden reserved for planting flowers to the area reserved for grass is $\dfrac{{24}}{{36}}$
$ = \dfrac{2}{3}$
Therefore, the required ratio is 2:3.
Note: Ratio is always taken of the quantity having similar units, that is why a ratio is always a unitless quality.
In this question also we’re asked the ratio of areas of two different places, since the area’s unit will remain the same and the ratio will come out to be a unitless value.