Question

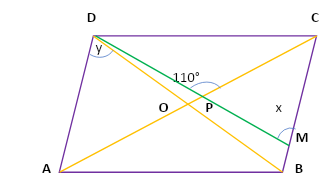
The given figure shows a rhombus ABCD in which angle $BCD = {80^ \circ }$. Find angles $x$ and $y$.

Answer 1

Hint: We will use the property of the rhombus which states that diagonals of a rhombus intersect each other at right angles. We will use another property that the diagonals of a rhombus bisect the vertex angles. We will consider triangles $\Delta DOA$ and $\Delta CPM$, using the angle sum property that the sum of all angles of a triangle is ${180^ \circ }$, we will calculate the value of $x$ and $y$.

Complete step-by-step answer:
We are given a rhombus ABCD and $\angle BCD = {80^ \circ }$.
We are required to find the value of the angles $x$ and $y$.
Now, we will use some properties of rhombus to calculate $x$ and $y$.
Property 1: The diagonals of a rhombus bisects the angles of the rhombus.
Property 2: Opposite angles of the rhombus are equal.
Property 3: The diagonals of a rhombus intersect each other at ${90^ \circ }$.

Using property 1, we can say that $\angle DCP = \angle MCP$.
And, $\angle DCP + \angle MCP = \angle BCD$.
So, we can write $\angle DCP + \angle MCP = {80^ \circ }$
$
   \Rightarrow 2\left( {\angle DCP} \right) = {80^ \circ } \\
   \Rightarrow \angle DCP = {40^ \circ } \\
   \Rightarrow \angle MCP = {40^ \circ } \\
 $
Now, using the Angle Sum Property (i.e., the sum of all interior angles of a triangle is ${180^ \circ }$) in the triangle CPM, we get
$ \Rightarrow \angle MCP + \angle CPM + \angle MPC = {180^ \circ }$
We know that DPM is a straight line, so $\angle DPC + \angle CPM = {180^ \circ }$
$
   \Rightarrow {110^ \circ } + \angle CPM = {180^ \circ } \\
   \Rightarrow \angle CPM = {70^ \circ } \\
 $
Substituting the value of $\angle MCP,\angle CPM{\text{ and }}\angle MPC$ in $\angle MCP + \angle CPM + \angle MPC = {180^ \circ }$, we get
$
   \Rightarrow {40^ \circ } + {70^ \circ } + x = {180^ \circ } \\
   \Rightarrow {110^ \circ } + x = {180^ \circ } \\
   \Rightarrow x = {70^ \circ } \\
 $
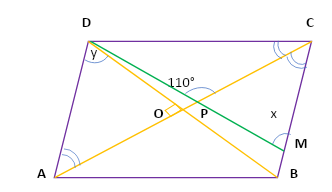
Now, from the Property 2, we can say that $\angle DCB = \angle DAB = {80^ \circ }$ and hence, $\angle DAO = {40^ \circ }$
And using the property 3, we can say that $\angle DOA = {90^ \circ }$.
Using the Angle Sum Property in \[\Delta DOA\], we have
$
   \Rightarrow \angle DAO + \angle DOA + \angle ADO = {180^ \circ } \\
   \Rightarrow {40^ \circ } + {90^ \circ } + y = {180^ \circ } \\
   \Rightarrow {130^ \circ } + y = {180^ \circ } \\
   \Rightarrow y = {50^ \circ } \\
 $
So, we get the value of $x{\text{ and }}y$ as $x = {70^ \circ }{\text{ and }}y = {50^ \circ }$.

Note:We have calculated the value of angles which are used in calculating $x{\text{ and }}y$ using the Angle sum property. Such questions are property based and can be tricky at various steps, for e.g., when we have used the straight angle DPM to calculate $\angle CPM$ and after that we have used it for calculating $x$.